Todos os anos, milhões de pessoas investem seus recursos financeiros apostando na mega-sena acreditando que as probabilidades estão a seu favor. Segundo uma base, desde o ano de 1996, houveram mais de 6.203.412.494 de apostas até o ano de 2023. Nesse sentido, decidi levantar algumas questões como:
- Quais são as reais probabilidades de vitória de todas as categorias de apostas que envolvem a mega-sena, como a quina, quadra e todas as faixas de dezenas?
- Existe alguma real vantagem financeira em fazer apostas com mais dezenas?
- Quanto dinheiro seria necessário investir para aumentar ao máximo as chances de uma vitória provavelmente certeira?
Regras do Mega-Sena
O conjunto de cada volante é composto por 60 números (chamados de dezenas), das quais o jogador deve escolher uma quantidade X para realizar um jogo que pode variar de 6 a 20 dezenas.
Um jogo padrão (ou simples) consiste em escolher 6 dezenas e a cada número adicional escolhido, você aumenta suas chances de vitória, ao passo que também aumenta o custo da aposta progressivamente.
Se o apostador, por exemplo, escolher 15 números, ele ganhará se 6 dentre esses 15 números forem os sorteados. Há prêmios também para a quina (5 acertos) e a quadra (4 acertos) que são menores obviamente.
Você pode deixar que o sistema escolha os números para você (Surpresinha) e/ou concorrer com a mesma aposta por 2, 4 ou 8 concursos consecutivos (Teimosinha).
A forma mais acessível de incrementar a probabilidade de vencer é apostar em bolões da Mega-Sena.
Premiação
O prêmio bruto corresponde a 43,35% da arrecadação. Dessa porcentagem:
- 35% são distribuídos entre os acertadores dos 6 números sorteados (Sena);
- 19% entre os acertadores de 5 números (Quina);
- 19% entre os acertadores de 4 números (Quadra);
- 22% ficam acumulados e são distribuídos aos acertadores dos 6 números nos concursos de final 0 ou 5.
- 5% ficam acumulados para a primeira faixa – sena – do último concurso do ano de final 0 ou 5 (Mega da Virada).
Estruturando o cálculo da probabilidade
Em primeiro lugar, como calculamos a probabilidade de vitória de cada tipo de jogo levando em consideração desde o jogo mais simples até os jogos com mais dezenas?
Como não importa a ordem em que esses números são sorteados, o cálculo da quantidade total de resultados possíveis é feito por meio de uma combinação de 60 elementos tomados 6 a 6 até 20 a 20.
Dessa forma, a seleção do conjunto {1, 2, 3, 4, 5, 6} para essa análise, significa o mesmo que {2, 3, 4, 1, 5, 6} assim como a seleção do conjunto {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20} significa o mesmo que {2, 3, 4, 1, 5, 6, 20, 17, 10, 9, 8, 7, 16, 14, 15, 18, 19, 11, 12, 13}
Então primeiro calculamos quantas combinações podemos formar escolhendo 6 números entre as 60 possibilidades e a partir dai, extrapolamos para os jogos com mais dezenas.
Para calcular as combinações, dentro da matemática probabilística, utilizamos uma fórmula de combinação simples (análise combinatória):
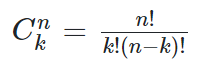
Para realizar o cálculo de probabilidade de um jogo simples, temos então:
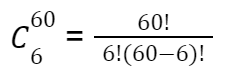
O resultado é 50.063.860, isso significa que existem 50.063.860 de possibilidades de se fazer um jogo com 6 números num volante de 60 números, ou seja, ao fazer um jogo simples, você tem 1 chance de vitória em 50.063.860, o que dá 0,000002% de probabilidade de vitória.
Mas isso é para um jogo simples, e como calculamos a probabilidade para as demais variáveis do jogo?
Dentro da categoria da sena, se formos realizar um jogo com 7 dezenas por exemplo, que é o próximo nível, se conseguirmos calcular quantas vezes maior é a probabilidade de vitória, basta dividirmos a probabilidade total do jogo simples por essa grandeza.
Calculamos então a combinação de 7 em 6 ou seja, quantas combinações de 6 números podem ser feitas com 7 números e temos C 7,6 = 7, onde a probabilidade de vitória de um jogo com 7 dezenas é 7 vezes maior do que um simples jogo com 6 dezenas.
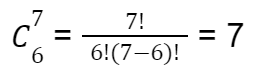
Já para calcular a probabilidade de se ganhar na quina ou na quadra, como nós precisamos de menos números para ganhar, significa que temos um saldo positivo de probabilidades dentro de cada categoria com a mesma dezena que fazemos o jogo da sena, então é mais fácil de se obter a vitória probabilisticamente (o prêmio em dinheiro também é menor).
Nesse caso temos para um jogo de 7 dezenas na quina a seguinte fórmula:
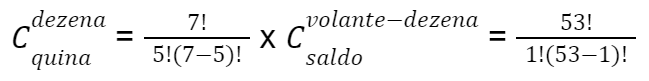
(C 7,5 = 21) x (C (60-7), 1 = 53) = 1.113, em seguida 50.063.860/1.113 resultando em 44.981 combinações possíveis, ou seja, 1 chance de vitória em 44.981 ou uma probabilidade de vitória de 0,00222% que é 1.113 maior do que um jogo simples da sena.
A partir dessa fórmula, como resultado final, calculando a probabilidade de vencer cada categoria (sena, quina e quadra) para todas as faixas de dezenas, temos a seguinte tabela, onde:
- Margem de grandeza: quantas vezes a probabilidade de vencer é maior do que um jogo simples da sena
- Probabilidade: Qual é a probabilidade de vencer, realizando um jogo com a quantidade de dezenas e categoria determinada (em porcentagem)
- Chances de ganhar: Qual é o número de combinações possíveis de se fazer realizando um jogo com a quantidade de dezenas e categoria determinada.
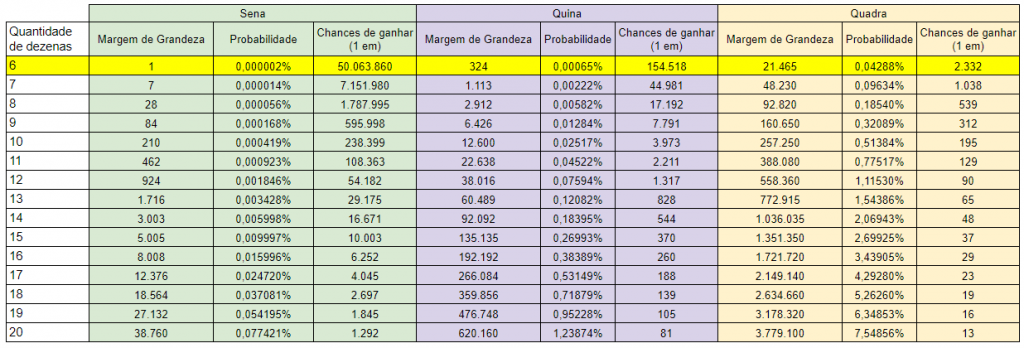
É interessante observar algumas coisas como o poder probabilístico de um jogo com 20 dezenas, que apesar se possui apenas 16 números a mais, aumenta suas chances de vitória em 38.760 vezes de ganhar a sena e reduz as possibilidades de combinações da quadra em apenas 13! É sem dúvidas o jogo mais poderoso.
Abaixo é possível observar como cada número de dezena adicional aumenta progressivamente a probabilidade de vitória.
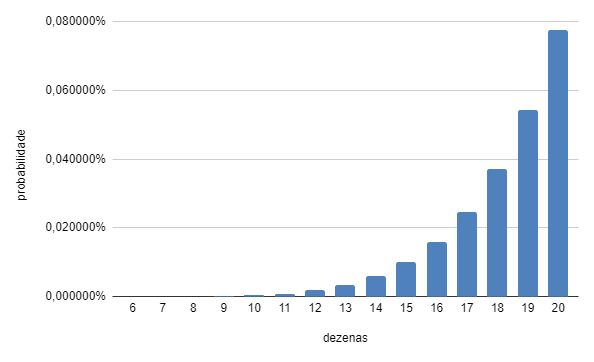
Vale mais a pena financeiramente fazer apostas com mais dezenas?
Quando se vai fazer um jogo, você escolhe quantas dezenas quer apostar. Ao escolher o menor número possível que é 6, conhecido como jogo simples, o preço do bilhete na lotérica é de R$4,50.
Ao tentar fazer um jogo com mais dezenas, o preço é mais caro e o motivo desse valor mais caro, é que ele segue uma ordem de grandeza proporcional à sua probabilidade de vitória como é possível perceber abaixo:
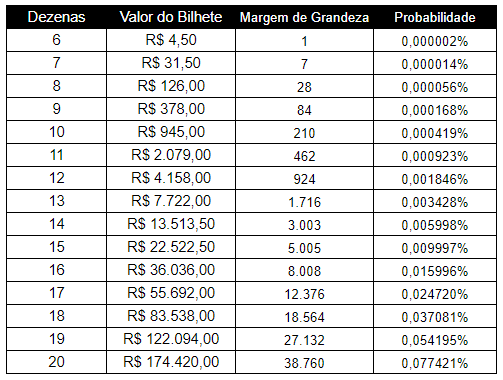
Um jogo com 7 dezenas te dá 7 vezes mais chances de vitória do que um jogo de 6, assim como um jogo de 8 dezenas te dá 28 vezes mais chances de vitória do que um de 6 e assim vai…
É interessante observar que antes de 2022 só era possível apostar até 15 dezenas e o jogo foi atualizado, saindo uma notificação no diário oficial aumentando o teto para 20 dezenas.
em meio a tantos números pode surgir a dúvida sobre o que é mais vantajoso estatisticamente falando, fazer diversos jogos simples ou investir direto em um jogo mais caro? Existe real vantagem financeiramente?
Como é possível observar na tabela, o preço de cada aposta é exatamente o valor de um bilhete simples multiplicado pela grandeza de probabilidades, nesse sentido, uma aposta com 10 dezenas, aumenta 210 vezes a sua probabilidade de vitória e portanto é 210 vezes mais caro do que um bilhete simples.
210 x R$4,50 = R$945,00
A resposta então é que não é mais vantajoso financeiramente fazer jogos com mais dezenas, pois estatisticamente o resultado é o mesmo, ou seja, pagar R$945,00 para fazer uma aposta com 10 dezenas garante a mesma probabilidade estatística de vitória do que fazer 210 apostas pagando R$4,50.
Quanto dinheiro é necessário investir para se obter 100% de chances de vitória e qual é o retorno sobre o investimento (ROI)?
É claro que na prática comprar todos os bilhetes para obter esse resultado seria impossível, não por questões financeiras, mas pelo simples fato de que não é possível impedir que as pessoas também comprem outros bilhetes (e provavelmente não é permitido pela regulamentação também), mas aqui iremos trabalhar no campo teórico.
Sabendo o preço de um bilhete de jogo básico e sua probabilidade de vitória, basta fazer uma regra de 3 onde:
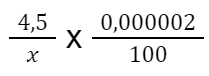
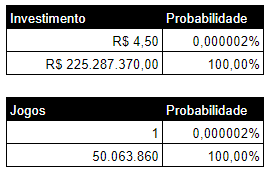
Na segunda tabela é possível obter uma validação onde 100% de probabilidade de vitória batem com o número total de combinações de um jogo simples.
A resposta é que seria necessário investir em média R$ 225.287.370,00 para se obter 100% de chances de vitória.
Esse investimento valeria a pena?
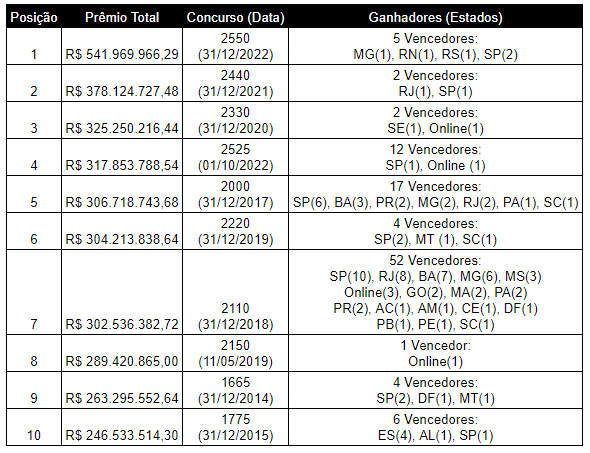
Observando uma tabela com os 10 maiores prêmios acumulados da mega-sena, é possível verificar que os valores são sempre superiores a R$ 225.287.370,00, nesses casos haveria um roi positivo em todos os casos.
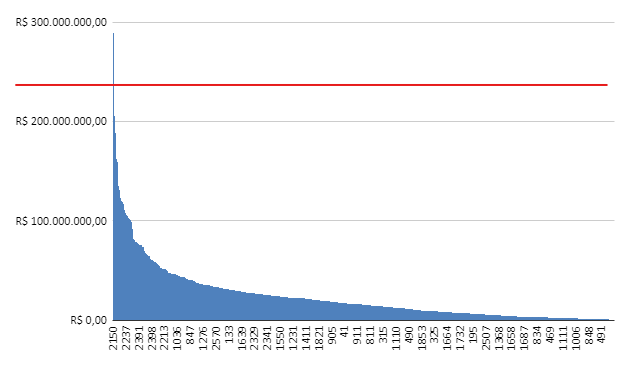
Porém essa não é a realidade para todos os concursos. Em caso de prêmios individuais por exemplo, conseguimos ver uma queda nítida e repentina nos valores das premiações e a partir da segunda premiação, já seria um prejuízo constatado.
Referências:
- https://loterias.caixa.gov.br/Paginas/Mega-Sena.aspx
- https://www.sorteonline.com.br/mega-sena/como-jogar
- https://pt.wikipedia.org/wiki/Combinat%C3%B3ria
- https://redeloteria.com.br/mega-sena/todos-os-resultados-da-mega-sena/29275
- https://www.lottoland.com/br/revista/os-ganhadores-e-maiores-premios-da-megasena.html


