O teste Z é um teste estatístico usado para determinar se há uma diferença significativa entre a média de uma amostra e a média de uma população, ou entre as médias de duas amostras, quando a variância populacional é conhecida. Ele é baseado na distribuição normal padrão.
Acesse este artigo para entender tudo sobre a teoria e prática de como utilizar a calculadora: https://datauniverse.com.br/teste-de-hipoteses/
Link para acessar a calculadora: https://docs.google.com/spreadsheets/d/1fqEo9cV8_hj4quDSBtzDYApWapca9q4Wd7HLgJ7-1sQ/copy
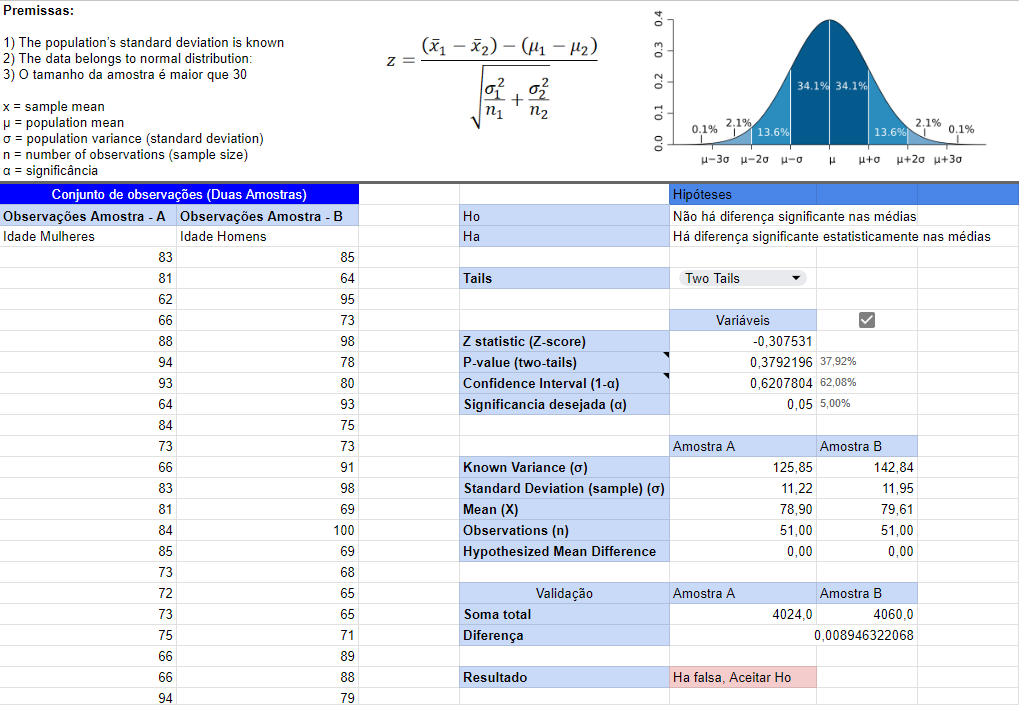
Como usar:
Basta preencher as duas colunas de observações das amostras manualmente com os próprios dados ou atualizar os dados aleatóriamente marcando e desmarcando a caixa:

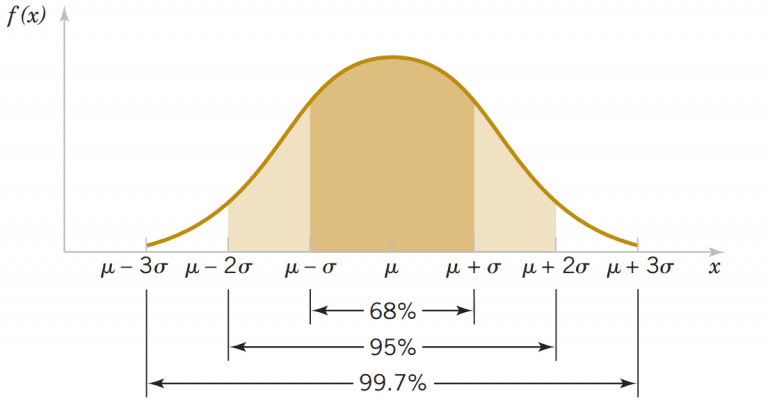
Gráficos de distribuição
Os gráficos de distribuição, ajudam a visualizar o formato da distribuição dos dados das observações das amostras A e B.

Uma distribuição estatística é uma função que descreve a frequência com que diferentes valores ocorrem em um conjunto de dados. Representa a maneira como os dados são distribuídos ao longo de um intervalo, e pode ser apresentada de várias formas, como distribuições normais, binomiais, uniformes, entre outras.
Ao analisar um gráfico de dispersão, você pode tomar decisões informadas sobre a natureza da relação entre variáveis, identificar anomalias e planejar próximas etapas na análise de dados.
Para que serve:
O teste Z é útil para:
- Comparar a média de uma amostra com uma média populacional conhecida.
- Comparar as médias de duas amostras independentes.
- Verificar hipóteses sobre proporções em amostras grandes.
Como funciona:
O teste Z segue os seguintes passos:
- Formulação das Hipóteses:
- Hipótese Nula (H₀): Afirma que não há diferença (por exemplo, a média da amostra é igual à média populacional).
- Hipótese Alternativa (Hₐ): Afirma que há uma diferença (por exemplo, a média da amostra é diferente da média populacional).
- Cálculo da Estatística Z:
Para uma amostra única:

Onde:
 | é a média da amostra |
 | é a média populacional |
 | é o desvio padrão populacional |
 | é o tamanho da amostra |
Para duas amostras:

Onde:
 | são as médias das amostras |
 | são as médias populacionais |
 | são os desvios padrão populacionais |
 | são os tamanhos das amostras |
- Determinação do P-valor:
- O P-valor é a probabilidade de obter um valor Z tão extremo ou mais extremo que o valor observado, assumindo que a hipótese nula é verdadeira.
- Para um teste bicaudal, calcula-se a probabilidade nas duas extremidades da distribuição normal.
- Comparação com o Nível de Significância (α):
- Se o P-valor é menor que α (por exemplo, 0,05), rejeita-se a hipótese nula.
- Se o P-valor é maior que α, não se rejeita a hipótese nula.
Exemplos de aplicação:
- Verificar se a média de altura dos estudantes de uma escola é diferente da média nacional.
- Comparar a eficácia de dois medicamentos com base em amostras de pacientes.
O teste Z é particularmente adequado quando o tamanho da amostra é grande (geralmente (n > 30)) e a variância populacional é conhecida. Se a variância populacional não é conhecida e a amostra é pequena, utiliza-se geralmente o teste t de Student.
Parâmetros estatísticos
- Hipótese Nula (H₀): É a hipótese inicial que assume que não há efeito ou diferença significativa entre os grupos ou condições em estudo. Geralmente, é a hipótese que se tenta refutar ou rejeitar.
- Hipótese Alternativa (Hₐ): É a hipótese que contrasta com a hipótese nula. Sugere que há um efeito significativo ou diferença entre os grupos ou condições em estudo. Aceitar Hₐ implica rejeitar H₀.
- Number of Tails: Refere-se ao tipo de teste estatístico baseado na hipótese alternativa. Pode ser:
- Unicaudal (one-tailed): Testa se um parâmetro é maior ou menor que um valor específico.
- Bicaudal (two-tailed): Testa se um parâmetro é diferente (maior ou menor) de um valor específico.
- Z Statistic (Z-score): É uma medida que descreve a posição de uma amostra em relação à média de uma distribuição normal padrão, medida em desvios padrão. Um Z-score indica quantos desvios padrão um valor está acima ou abaixo da média.
- P-value (two-tails): É a probabilidade de observar um valor extremo ou mais extremo do que o observado, assumindo que a hipótese nula é verdadeira. Em um teste bicaudal, considera as extremidades de ambas as caudas da distribuição.
- Intervalo de Confiança (1-α): É um intervalo estimado a partir dos dados da amostra, dentro do qual se espera que o parâmetro populacional verdadeiro esteja, com um nível de confiança de (1-α)%. Por exemplo, um intervalo de confiança de 95% significa que temos 95% de certeza de que o parâmetro verdadeiro está dentro desse intervalo.
- Significância Desejada (α): É o nível de significância pré-definido para um teste estatístico, representando a probabilidade de cometer um erro do Tipo I (rejeitar a hipótese nula quando ela é verdadeira). Comumente, α é 0,05 ou 5%.
- Variância Conhecida (σ): Refere-se à variância da população que é conhecida ou assumida conhecida, usada em testes estatísticos como o teste Z.
- Desvio Padrão da Amostra (σ): É uma medida de dispersão que indica o quanto os valores de uma amostra variam em relação à média da amostra.
- Média (X̄): É a soma de todos os valores da amostra dividida pelo número de observações. Representa a média aritmética dos dados da amostra.
- Observações (n): Refere-se ao número total de dados ou pontos de amostra coletados em um estudo.
- Diferença de Média Hipotetizada: É a diferença entre as médias populacionais que se espera ou se assume existir sob a hipótese alternativa.
- Soma Total de Observações na Amostra: Refere-se à soma de todos os valores observados na amostra.
- Diferença entre as Amostras: Refere-se à diferença observada entre as médias ou proporções de duas ou mais amostras.
- Decisão Estatística a ser Tomada quando Hₐ é Falsa, Aceitar H₀: Significa que, com base nos resultados do teste estatístico, não há evidência suficiente para rejeitar a hipótese nula, então aceitamos H₀ como verdadeira (ou não rejeitamos H₀).
Esses parâmetros são essenciais para conduzir e interpretar testes estatísticos, ajudando a determinar a significância dos resultados de pesquisas e experimentos.