Em uma manhã do ano de 1968, por volta das 11h30, Juanita Brooks estava voltando para casa depois de fazer compras. Enquanto ela caminhava por um beco, alguém a empurrou para o chão e pegou sua bolsa. Quando ela olhou para cima, ela viu uma jovem branca com cabelos loiros fugindo.
Um vizinho relatou que viu uma mulher branca com cabelos loiros em um rabo de cavalo sair correndo do beco e entrar em um carro amarelo. O carro, dirigido por um homem afro-americano de bigode e barba, acelerou e fugiu daquela cena.
Um policial com as característica e a pista acima foi à casa de um casal tido como suspeito chamados de Malcolm e Janet Collins quatro dias depois e viu um carro amarelo estacionado ali. Ao interrogar o casal, viu Janet, que era branca, tinha cabelos loiros escuros presos em um rabo de cavalo. Malcolm, que era afro-americano, tinha bigode e disse que às vezes usava barba, mas a havia raspado três semanas antes.
Janet disse que, no dia do roubo, ela trabalhava como empregada doméstica em um endereço próximo ao local do roubo, mas estava trabalhando no momento do ato. A mulher para quem Janet trabalhava, no entanto, disse que Janet saiu do trabalho por volta das 11h30 e foi buscada por Malcolm em um carro amarelo.
Os Collinses foram acusados de roubo em segundo grau no tribunal estadual. Eles se declararam inocentes e tiveram um julgamento com júri conjunto. No julgamento, o caso da promotoria foi baseado em grande parte em evidências de que as aparições de Janet e Malcolm em seu carro correspondiam à descrição das testemunhas oculares dos perpetradores e seu carro de fuga.
Para reforçar essa evidência circunstancial, o promotor chamou um professor de matemática da faculdade, que contou aos jurados sobre o conceito estatístico chamado regra do produto. Essa regra estabelece que a probabilidade da ocorrência conjunta de múltiplos fatores mutuamente independentes é igual ao produto das probabilidades individuais de todos os fatores.
O promotor então pediu ao professor que usasse a regra para calcular a probabilidade das características relevantes com base nas suposições fornecidas pelo promotor. Essas suposições incluíam:

A probabilidade combinada de todos esses eventos é de P (A∩B) = P (A)*P (B) o que resulta em 0,000000083 ou 1 em 12 milhões.
O promotor não ofereceu nenhuma evidência para apoiar as probabilidades dos vários fatores individuais que ele forneceu. Com base nessas suposições, e na probabilidade calculada pelo professor, o tribunal de primeira instância rejeitou a objeção do advogado de defesa ao testemunho do professor e o júri condenou os Collins. Michael apelou então para a Suprema Corte da Califórnia.
Prosecutor’s fallacy (falácia do promotor)
A Suprema Corte da Califórnia anulou a condenação, criticando o raciocínio estatístico por ignorar dependências entre as características, por exemplo, homens barbudos geralmente usam bigodes, e portanto os fatores nesse caso não seriam totalmente independentes, mas mútuos.
O tribunal observou que a inferência estatística correta seria a probabilidade de que nenhum outro casal que pudesse ter cometido tal roubo tivesse as mesmas características dos réus, dado que pelo menos um casal tinha as características identificadas. O tribunal observou, em um apêndice à sua decisão, que usando essa inferência estatística, mesmo que as estatísticas do promotor fossem todas corretas e independentes como ele presumia, a probabilidade de os réus serem inocentes seria superior a 40%.
Essa inferência equivocada, comumente chamada de Prosecutor’s fallacy (falácia do promotor), iguala incorretamente a probabilidade de que um réu aleatório tenha certas características com a chance de que o réu seja culpado.
Esse nome advém do uso comum por promotores para exagerar a probabilidade de culpa de um réu criminal. A falácia também pode ser usada para apoiar outras alegações, incluindo a inocência de um réu.
Tal falácia é uma falha do raciocínio estatístico envolvendo um teste para uma ocorrência, como uma correspondência de DNA por exemplo. Um resultado positivo no teste pode paradoxalmente ser mais provável de ser um resultado errôneo do que uma ocorrência real, mesmo que o teste seja muito preciso.
A falácia básica resulta do mal entendimento sobre probabilidade condicional e da negligência das probabilidades anteriores de um réu ser culpado antes que a evidência fosse apresentada. Quando um promotor coleta algumas evidências (por exemplo, uma correspondência de DNA) e faz um especialista testemunhar que a probabilidade de encontrar essas evidências se o acusado for inocente é pequena, a falácia ocorre se for concluído que a probabilidade de o acusado ser inocente deve ser comparativamente pequena.
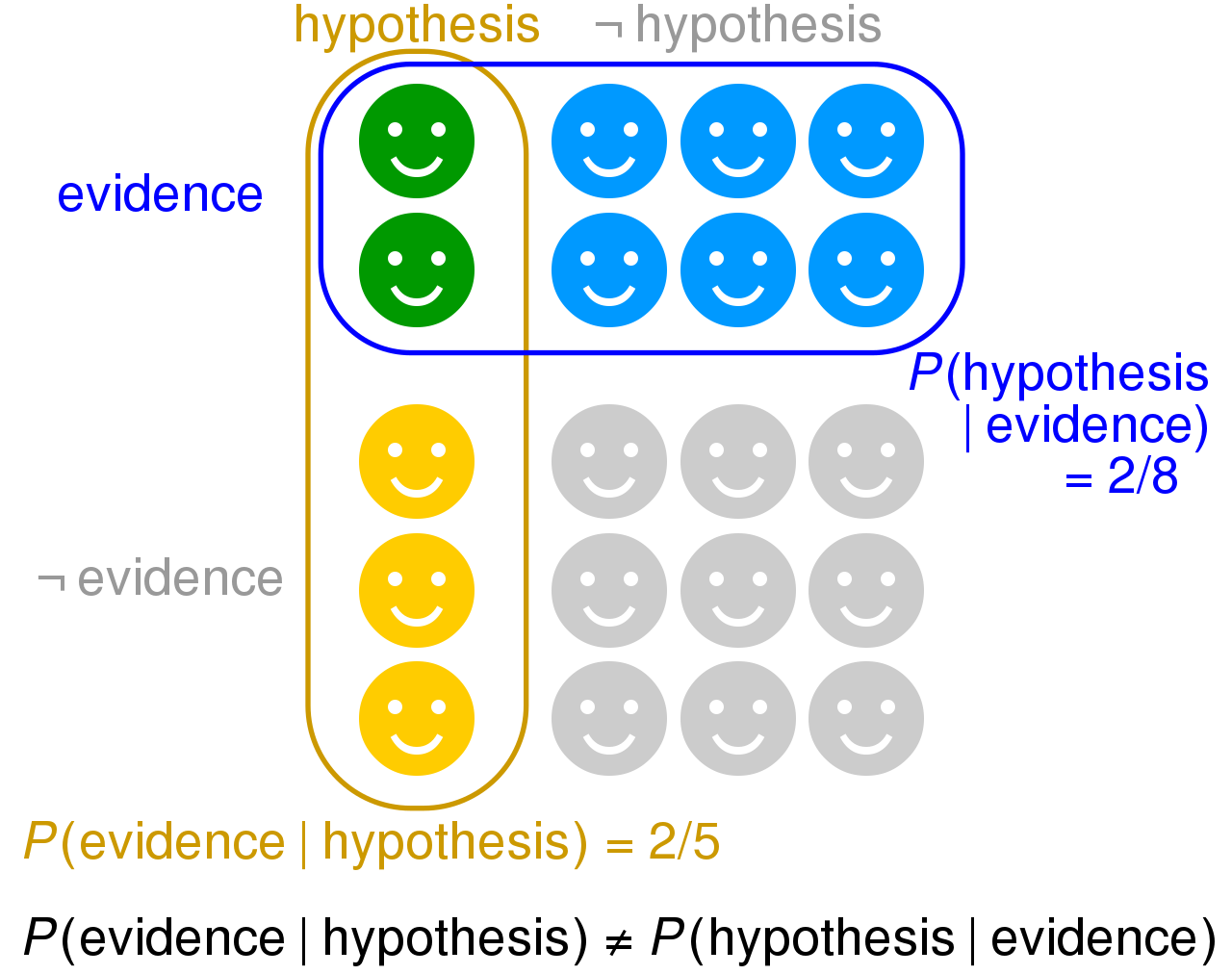
Neste gráfico acima, para ilustrar a ocasião, a hipótese é a possibilidade de o réu ser culpado, enquanto as evidências encontradas se referem a um resultado positivo de teste, como DNA ou tipo sanguíneo compatível. Embora a probabilidade de encontrar evidências do verdadeiro culpado possa ser bastante alta (nesse caso, dois quintos, ou 40%), a probabilidade de um determinado indivíduo ser culpado dado que neles foram encontradas tais provas não tem relação com a primeira, e muitas vezes será muito menor (nesse exemplo, apenas dois oitavos, ou 25%).
Se a correspondência de DNA for usada para confirmar a culpa da qual se suspeita, então é de fato uma forte evidência. No entanto, se a evidência de DNA for a única evidência contra o acusado e o acusado foi escolhido em um grande banco de dados de perfis de DNA, as chances de a correspondência ser feita aleatoriamente podem ser aumentadas e menos prejudiciais ao réu. As probabilidades neste cenário não se relacionam com as probabilidades de ser culpado, mas sim com as probabilidades de ser escolhido aleatoriamente.
Por exemplo, se o autor de um crime for conhecido por ter o mesmo tipo sanguíneo de um determinado réu e 10% da população compartilhar esse tipo sanguíneo, então uma versão da falácia do promotor seria alegar que, com base apenas nisso, a probabilidade que o réu é culpado é de 90%.
No entanto, esta conclusão só está próxima de correta se o réu foi selecionado como o principal suspeito com base em evidências robustas descobertas antes do exame de sangue e não relacionadas a ele (a correspondência de sangue pode então ser uma “coincidência inesperada”). Caso contrário, o raciocínio apresentado é falho, pois ignora a alta probabilidade anterior (isto é, antes do exame de sangue) de que ele seja uma pessoa inocente aleatória.
Suponha, por exemplo, que 1.000 pessoas vivam na cidade onde ocorreu um assassinato. Isso significa que vivem lá 100 pessoas que têm o tipo de sangue do assassino; portanto, a verdadeira probabilidade de que o réu seja culpado – com base no fato de que seu tipo de sangue corresponde ao do assassino – é de apenas 1%, muito menos do que os 90% argumentados pelo promotor.
Falácia do Argumento da raridade
Suponha que um ganhador da Mega Sena é acusado de trapacear, com base na improbabilidade de ganhar. No julgamento, o promotor calcula a probabilidade 1 em 50.063.000 de ganhar na loteria sem trapacear e argumenta que essa é a probabilidade de inocência.
A falha lógica é que o promotor não conseguiu explicar o grande número de pessoas que jogam na loteria. Embora a probabilidade de qualquer pessoa ganhar seja bastante baixa, a probabilidade de qualquer pessoa ganhar na loteria, dado o número de pessoas que jogam, é muito alta.
A correta utilização das estatísticas probabilísticas nesses casos então, é somente reforçar uma pré existente suspeita forte contra um réu e nunca utilizar a baixa probabilidade de inocência / culpa como argumento primário na decisão judicial.
Por conta desse erro de interpretação, por volta de 1996, quatro mães britânicas foram presas por assassinato porque dois ou mais de seus bebês morreram em seus berços. Três das mães foram condenadas e sentenciadas à prisão perpétua. No entanto, em 2006, todas as quatro mães foram declaradas inocentes de crimes que nunca haviam ocorrido.
O caso de Sally Clark e o teorema de Bayes
Sally Clark, uma advogada que perdeu seu primeiro filho com 11 semanas e o segundo com 8 semanas, foi condenada em 1999. Um proeminente pediatra, Sir Roy Meadow, testemunhou na acusação sobre a Síndrome da Morte Súbita Infantil, conhecida como SIDS nos Estados Unidos e morte no berço na Grã-Bretanha. Citando um estudo do governo, Meadow disse que a incidência de morte por SIDS era de uma em 8.500 em uma família como a de Clark (estável, rica, não fumante, com uma mãe com mais de 26 anos).
No entanto, apesar do fato de algumas famílias serem predispostas à SIDS, Meadow presumiu erroneamente que a morte de cada irmão ocorreu independentemente da outra.
Calculando a probabilidade conjunta de P (A∩B) = 8.500 * 8.500 = 72.250.000 chegou a conclusão que a chance de duas crianças morrerem em uma família como a de Sally Clark era tão rara (1/72.250.000) que era mais provável que elas tivessem sido assassinadas.
Porém nesse e em muitos outros casos, uma simples probabilidade conjunta não é evidência suficiente para suportar a hipótese de culpa ou inocência de um réu, é para isso que existe a ferramenta da análise bayesiana, a qual teria mostrado que as crianças provavelmente morreram de SIDS.
O Teorema de Bayes, em homenagem ao matemático britânico do século XVIII Thomas Bayes, é uma fórmula matemática para determinar a probabilidade condicional. Probabilidade condicional é a probabilidade de um resultado ocorrer, com base em um resultado anterior ocorrido em circunstâncias semelhantes. O teorema de Bayes fornece uma maneira de revisar previsões ou teorias existentes (atualizar probabilidades) dadas evidências novas ou adicionais.
Através de uma árvore de probabilidades, nós atualizamos ou revisamos as previsões de cada nó de acordo com as evidências posteriores:

Assim, a questão perante o tribunal deveria ter sido: os bebês provavelmente morreram de causas naturais ou assassinato?
Primeiro, examinamos as causas naturais da morte infantil súbita. A chance de um bebê aleatório morrer de SIDS era de cerca de 1 em 1.300 durante esse período na Grã-Bretanha. O argumento de Meadow era falho e produzia uma chance muito menor de morte natural. As probabilidades estimadas de uma segunda morte por SIDS na mesma família eram muito maiores, talvez uma em 100, porque os membros da família podem compartilhar uma predisposição ambiental ou genética comum para SIDS.
Em segundo lugar, nos voltamos para a hipótese de que os bebês foram assassinados. Apenas cerca de 30 crianças de 650.000 nascimentos anuais na Inglaterra, Escócia e País de Gales foram assassinadas por suas mães. O número de duplos assassinatos deve ser muito menos provável, estimado em 10 vezes menos provável.
Segundo a fórmula de Bayes:

Tomamos a hipótese “H” a ser atualizada como sendo: os dois filhos de Sally Clark morreram de SIDS. O dado “D” será que ambas as crianças morreram repentina e inesperadamente. As probabilidades iniciais que entram na regra de Bayes são P(H) e seu oposto, P(nãoH). Como discutido acima, P(H) é considerado como tendo o valor
P(H) = 1/1300 × 1/100 = 0,0000077
A alternativa P(nãoH) é então dada por
P(nãoH) = 1 – P(H) = 0,9999923
Agora olhamos para os dados. Ele figura nas probabilidades P(D | H) e P(D | nãoH). O primeiro é igual a um, pois é a probabilidade de as crianças terem morrido repentina e inesperadamente, dado que morreram de SIDS. P(D | nãoH) é a probabilidade de que um par aleatório de irmãos morra repentina e inesperadamente, mas não de SIDS. A promotoria vai equiparar isso a assassinato. A estimativa feita no parágrafo acima foi
P(D | nãoH) = 30/650000 × 1/10 = 0,0000046.
O objetivo é estimar P(H | D), a probabilidade de que a causa da morte tenha sido SIDS, dadas suas mortes inexplicáveis.
P(H | D) = 1 × 0.0000077 / 1 × 0.0000077 + 0.999992 × 0.0000046 ≈ 0.6
Concluímos então que é mais provável que as crianças tenham morrido de SIDS
Conclusão
A falácia do promotor acabou ficando muito famosa principalmente pelo impacto negativo que o mau uso das ferramentas e da interpretação estatística causou na vida de diversas mulheres nos Estados Unidos.
Considerando que esses casos ganharam notoriedade e atenção da mídia, poderíamos imaginar quantas pessoas já foram injustiçadas por falácias no tribunal de justiça.
Entendendo a falácia do argumento de raridade, fica mais claro o quão injusto e incorreto é cometer o erro da falácia do promotor utilizando deste argumento pois o simples fato de uma probabilidade ser baixa não deve ser entendida como a probabilidade remota de inocência de um réu, mas deve ser entendida apenas e somente como a probabilidade daquele evento ocorrer aleatoriamente. Deve ser conciliado a isso o fato de que quando analisamos as probabilidades de um universo com uma população de um país inteiro, calcular a probabilidade de qualquer evento deve retornar números extremamente baixos, pois são muitas as variáveis que se cruzam em eventos aleatórios.
O que é importante levar de tudo isso é que a estatística deve ser utilizada como um argumento complementar no julgamento de réus e nunca como uma prova definitiva de um evento.
Referências:


