Detalhes do projeto
- Link do projeto no Github: https://github.com/cerqueiralex/project-personal-prisioners-dilemma
- Tecnologias: Python, Tensorflow, Random, Deep Q-Learning (DQN)
- Categorias: Data Science, Machine Learning
A Teoria dos Jogos (Game Theory) é um campo da matemática e da economia que estuda como indivíduos ou grupos tomam decisões estratégicas em cenários onde suas escolhas afetam uns aos outros.
Esses “jogos” envolvem situações onde o resultado de cada jogador depende das ações dos outros, e a teoria busca entender as melhores estratégias para cada participante.
É amplamente aplicada em economia, psicologia, ciência política e até mesmo em biologia evolutiva para entender desde competições de mercado até comportamentos sociais.
O Dilema dos Prisioneiros
O Dilema dos Prisioneiros é um dos exemplos mais conhecidos da Teoria dos Jogos. Nele, dois suspeitos de um crime são presos e mantidos separados. Cada um tem duas opções: confessar ou não confessar o crime. As possíveis consequências são as seguintes:
- Se ambos não confessarem, cada um pega uma pena leve (digamos, 1 ano).
- Se um confessar e o outro não confessar, o que confessou fica livre, enquanto o que não confessou recebe a pena máxima (10 anos).
- Se ambos confessarem, cada um recebe uma pena moderada (5 anos).
Os prisioneiros não conseguem se comunicar e precisam tomar suas decisões sem saber o que o outro vai escolher.
Isso cria um dilema: embora a melhor estratégia conjunta seja ambos não confessarem (levando a penas mínimas para ambos), o medo de que o outro possa confessar leva cada prisioneiro a considerar confessar como uma opção mais segura, pois, se o outro confessar, ao menos evitará a pena máxima.
Esse dilema gira em torno de um tema extremamente importante dentro da nossa sociedade: Confiança!
Relação entre Teoria dos Jogos e o Dilema dos Prisioneiros
O Dilema dos Prisioneiros demonstra um conceito importante na Teoria dos Jogos chamado equilíbrio de Nash. Esse equilíbrio ocorre quando, em uma situação com múltiplos jogadores, ninguém pode melhorar seu resultado mudando de estratégia, desde que os outros jogadores mantenham suas escolhas.
No dilema, o equilíbrio de Nash é que ambos confessem, pois, dado que um prisioneiro está confessando, o outro não ganha nada ao ficar em silêncio.
Esse exemplo ajuda a ilustrar uma verdade fundamental na Teoria dos Jogos: os interesses individuais e os interesses coletivos nem sempre estão alinhados.
Situações como o Dilema dos Prisioneiros são comuns em mercados, política e comportamento social, onde decisões baseadas apenas no próprio interesse individual podem levar a resultados subótimos para todos.
Primeiro experimento: Testando partidas aleatórias
Antes de fazer um treinamento de modelo, resolvi testar como seria o comportamento de escolhas aleatórias.
Para isso foi construido esse código onde cada prisioneiro, aleatóriamente escolhe entre cooperar “cooperate” ou trair “betray”.
import random
import matplotlib.pyplot as plt # Importando a biblioteca para gráficos
# Definir número de rodadas
rounds = 1000
# Pontuação acumulada para cada prisioneiro
score_prisoner1 = 0
score_prisoner2 = 0
# Listas para armazenar as pontuações acumuladas ao longo das rodadas
scores_prisoner1 = []
scores_prisoner2 = []
# Função para simular uma rodada do dilema dos prisioneiros
def play_round():
# Cada prisioneiro escolhe aleatoriamente entre "cooperar" ou "trair"
choice1 = random.choice(["cooperate", "betray"])
choice2 = random.choice(["cooperate", "betray"])
if choice1 == "cooperate" and choice2 == "cooperate":
return 3, 3, choice1, choice2 # Ambos cooperam
elif choice1 == "betray" and choice2 == "betray":
return 1, 1, choice1, choice2 # Ambos traem
elif choice1 == "cooperate" and choice2 == "betray":
return 0, 5, choice1, choice2 # Prisioneiro 1 coopera, Prisioneiro 2 trai
else:
return 5, 0, choice1, choice2 # Prisioneiro 1 trai, Prisioneiro 2 coopera
# Executa os rounds, acumula pontuação e exibe cada rodada
for round_num in range(1, rounds + 1):
points1, points2, choice1, choice2 = play_round()
score_prisoner1 += points1
score_prisoner2 += points2
# Armazenar pontuações acumuladas
scores_prisoner1.append(score_prisoner1)
scores_prisoner2.append(score_prisoner2)
# Exibir resultados da rodada
print(f"Rodada {round_num}:")
print(f" Prisioneiro 1 escolheu: {choice1} | Pontos nesta rodada: {points1}")
print(f" Prisioneiro 2 escolheu: {choice2} | Pontos nesta rodada: {points2}")
print(f" Pontuação acumulada - Prisioneiro 1: {score_prisoner1}, Prisioneiro 2: {score_prisoner2}")
print("-" * 40)
# Resultados finais
print("Resultado Final:")
print(f"Pontuação final do Prisioneiro 1: {score_prisoner1}")
print(f"Pontuação final do Prisioneiro 2: {score_prisoner2}")
# Gerar gráfico da pontuação acumulada ao longo dos rounds
plt.figure(figsize=(12, 6))
plt.plot(scores_prisoner1, label="Prisioneiro 1", color='red')
plt.plot(scores_prisoner2, label="Prisioneiro 2", color='blue')
plt.title("Evolução da Pontuação Acumulada dos Prisioneiros")
plt.xlabel("Rodadas")
plt.ylabel("Pontuação Acumulada")
plt.legend()
plt.grid()
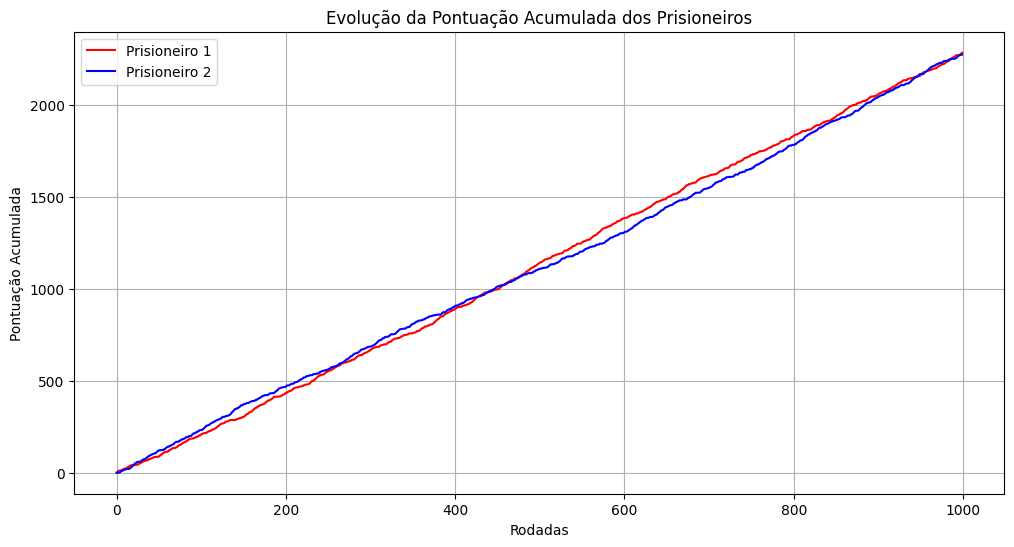
plt.show()Esse é o resultado de 5 partidas aleatórias, onde ocorreram 2 vitórias para o prisioneiro 2 e 3 vitórias para o prisioneiro 1:
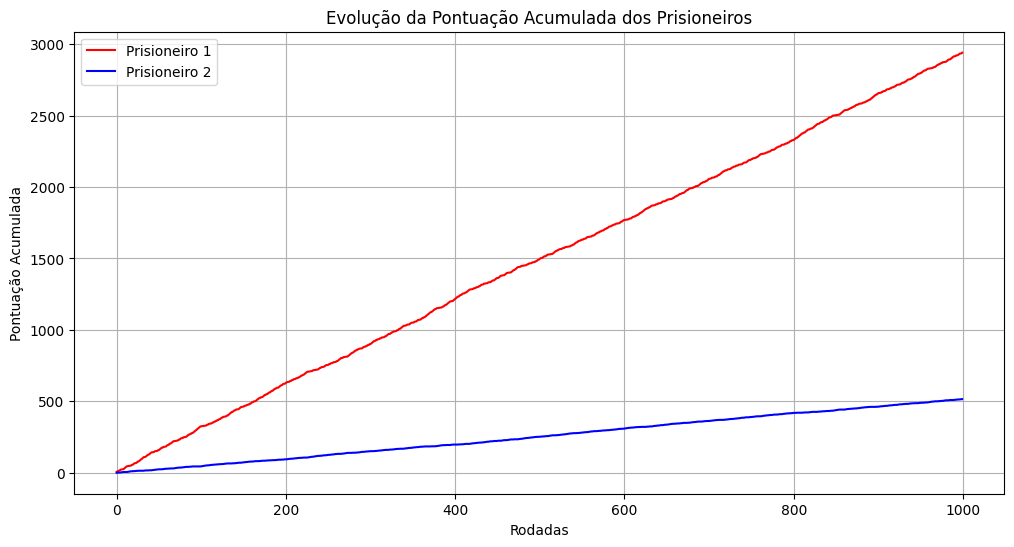
Olhando para o gráfico abaixo, é possível observar que no comportamento aleatório, o acúmulo das pontuações está sempre muito próximo, o que é esperado.
Pela projeção de 1000 rodadas, é possível verificar que não é uma boa estratégia e que a chance de vitória é sempre de 50%, mas esse gráfico é interessante para compreender as próximas etapas.
Desenvolvendo o código em Python utilizando tensorflow.keras
A lógica que foi desenvolvida acontece de forma que somente o primeiro prisioneiro irá receber o treinamento de aprendizado por reforço com Q-Learning enquanto que o segundo prisioneiro sempre irá tomar decisões aleatórias.
A ideia é que o primeiro prisioneiro aprenda a melhorar sua estratégia conforme ele aprende com as decisões do segundo.
Para implementar o Q-Learning usando TensorFlow (TF), vamos usar uma rede neural para aproximar a função Q. Esse método é conhecido como Deep Q-Learning (DQN) e é útil para problemas com espaço de estado grande ou contínuo, onde o uso de uma tabela Q tradicional seria inviável.
Neste exemplo do Dilema dos Prisioneiros, vamos configurar uma rede neural simples para estimar a Q-valor para cada ação (“cooperar” ou “trair”) com base na última ação do outro prisioneiro. Essa rede será treinada usando a biblioteca TensorFlow.
Para a Construção do Modelo Q, usamos uma rede neural de três camadas (duas ocultas e uma de saída) para prever o valor Q para cada ação. A entrada é o estado atual, que inclui a última ação do Prisioneiro 2 representada como um vetor one-hot.
# Parâmetros do aprendizado
learning_rate = 0.01
discount_factor = 0.9
exploration_rate = 1.0
exploration_decay = 0.01
min_exploration_rate = 0.01
rounds = 1000
# Pontuação acumulada para cada prisioneiro
score_prisoner1 = 0
score_prisoner2 = 0
# Contadores de escolhas para cada prisioneiro
choices_count = {
"prisoner1": {"cooperate": 0, "betray": 0},
"prisoner2": {"cooperate": 0, "betray": 0}
}
# Definir ações
actions = ["cooperate", "betray"]
# Converter ações para índices
action_to_index = {action: i for i, action in enumerate(actions)}
# Construir a rede neural para aproximar a função Q
def build_model(input_size, output_size):
model = Sequential([
Dense(24, input_dim=input_size, activation="relu"),
Dense(24, activation="relu"),
Dense(output_size, activation="linear")
])
model.compile(optimizer=Adam(learning_rate=learning_rate), loss="mse")
return model
# Modelo Q para o Prisioneiro 1
model = build_model(input_size=2, output_size=len(actions))
# Função para simular uma rodada do dilema dos prisioneiros
def play_round(prisoner1_choice, prisoner2_choice):
if prisoner1_choice == "cooperate" and prisoner2_choice == "cooperate":
return 3, 3 # Ambos cooperam
elif prisoner1_choice == "betray" and prisoner2_choice == "betray":
return 1, 1 # Ambos traem
elif prisoner1_choice == "cooperate" and prisoner2_choice == "betray":
return 0, 5 # Prisioneiro 1 coopera, Prisioneiro 2 trai
else:
return 5, 0 # Prisioneiro 1 trai, Prisioneiro 2 coopera
# Função para escolher a ação do Prisioneiro 1
def choose_action(state):
if np.random.rand() < exploration_rate:
# Exploração: escolhe uma ação aleatória
return random.choice(actions)
else:
# Exploração: escolhe a ação com maior valor Q estimado
q_values = model.predict(state)
return actions[np.argmax(q_values[0])]
# Executa os rounds
last_prisoner2_choice = random.choice(actions)
for round_num in range(1, rounds + 1):
# Estado atual (última ação do Prisioneiro 2 em one-hot encoding)
state = np.array([[1 if last_prisoner2_choice == action else 0 for action in actions]])
# Escolher a ação do Prisioneiro 1
prisoner1_choice = choose_action(state)
prisoner2_choice = random.choice(actions)
# Contabilizar as escolhas
choices_count["prisoner1"][prisoner1_choice] += 1
choices_count["prisoner2"][prisoner2_choice] += 1
# Jogar a rodada e obter a recompensa
points1, points2 = play_round(prisoner1_choice, prisoner2_choice)
score_prisoner1 += points1
score_prisoner2 += points2
# Próximo estado
next_state = np.array([[1 if prisoner2_choice == action else 0 for action in actions]])
# Atualização do Q-valor
target = points1 + discount_factor * np.max(model.predict(next_state)[0])
target_f = model.predict(state)
target_f[0][action_to_index[prisoner1_choice]] = target
# Treinar o modelo
model.fit(state, target_f, epochs=1, verbose=0)
# Atualizar a última escolha do Prisioneiro 2 para a próxima rodada
last_prisoner2_choice = prisoner2_choice
# Decaimento da taxa de exploração
exploration_rate = max(min_exploration_rate, exploration_rate * exploration_decay)Escolha de Ação:
A função choose_action usa uma política ε-greedy para escolher uma ação com base na previsão do modelo Q. Durante o treinamento, o agente explora mais, e com o tempo passa a explorar menos à medida que aprende.
Atualização do Q-valor e Treinamento do Modelo:
Após cada rodada, calculamos o alvo para a ação escolhida, que é o valor de recompensa somado ao valor Q máximo esperado para o próximo estado. Esse valor é então usado para ajustar o modelo.
Decaimento da Taxa de Exploração:
Após cada rodada, a taxa de exploração diminui, incentivando o agente a explorar menos conforme aprende.
Este modelo aproxima o comportamento de um agente Q-Learning com aprendizado por reforço, mas utiliza uma rede neural para aprender Q-valores ao invés de uma tabela Q.
Motivos para o Decaimento da Taxa de Exploração
A taxa de exploração no aprendizado por reforço decai com o tempo para permitir que o agente aprenda a explorar menos conforme ele acumula conhecimento do ambiente e explorar mais as ações que têm maior potencial de recompensa.
Se a taxa de exploração subisse com o tempo, o agente continuaria a tomar ações de forma aleatória mesmo quando ele já tivesse uma estratégia razoavelmente boa, o que impediria que ele convergisse para uma política estável.
Exploração Inicial:
No início do treinamento, o agente tem pouca ou nenhuma informação sobre quais ações são melhores. Uma alta taxa de exploração (ε) permite que o agente experimente várias ações, conheça o ambiente e construa uma base inicial de conhecimento.
Exploração x Exploração:
Conforme o treinamento avança, o agente já terá acumulado experiência e aprendido quais ações tendem a dar melhores recompensas. Se a taxa de exploração permanecer alta, o agente continuará a tomar decisões aleatórias, reduzindo a efetividade do aprendizado.
Diminuindo a exploração, o agente passa a confiar mais em seu aprendizado (exploração) e a escolher as ações que parecem mais promissoras com base nos valores Q já aprendidos.
Convergência para uma Política Ótima:
O objetivo é que, ao final do treinamento, o agente seja capaz de seguir uma política ótima, ou seja, uma estratégia onde ele maximiza suas recompensas.
Um ε próximo de zero é desejável ao fim do treinamento, pois indica que o agente seguirá a política que ele acredita ser ótima, baseada nas recompensas que ele acumulou ao longo do tempo.
Primeiros Rounds
Nos primeiros rounds é possível observar que com uma taxa de exploração alta, o primeiro prisioneiro fica bem atrás do segundo nas pontuações e isso acontece até mais ou menos a rodada 50 onde el começa a aprender os padrões:
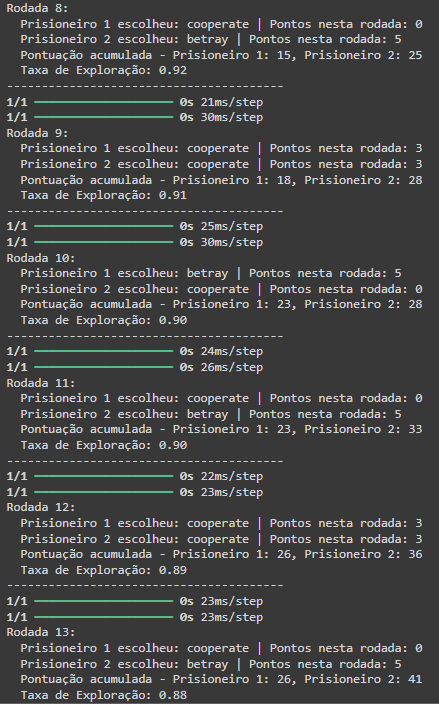
Resultados do treinamento com 1000 rounds
Ao final do treinamento com 1000 rodadas o prisioneiro 1 consegue aprender que quanto mais ele escolher a opção de betray, mais ele aumenta as chances de ganhar.
Mesmo realizando diversos testes, o comportamento do aprendizado é o mesmo! Sempre que o prisioneiro 1 aprende que betray é a melhor estratégia por volta da rodada 50, ele começa a ganhar e disparar na pontuação.
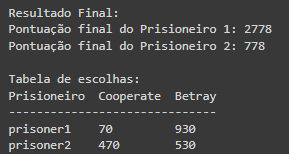
Ao final conseguimos visualizar a curva de aprendizado do prisioneiro 1
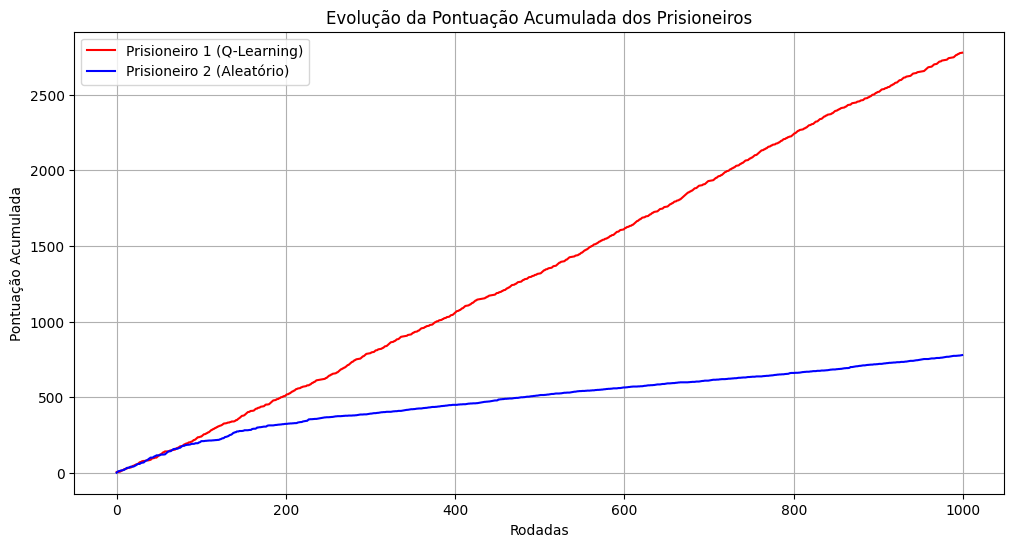
Porque sempre escolher a opção de betray é matematicamente a estratégia predominante?
Escolher a opção de “betray” (trair) no Dilema dos Prisioneiros é matematicamente vantajoso devido à análise de recompensas associadas a cada combinação de decisões dos prisioneiros. Vamos detalhar essa análise.
Cenário do Dilema dos Prisioneiros
Considere duas opções para cada prisioneiro: cooperate (cooperar) ou betray (trair). A tabela a seguir mostra as recompensas associadas a cada combinação de decisões:
| Prisioneiro 1 | Prisioneiro 2 | Pontuação P1 | Pontuação P2 |
|---|---|---|---|
| Cooperate | Cooperate | 3 | 3 |
| Cooperate | Betray | 0 | 5 |
| Betray | Cooperate | 5 | 0 |
| Betray | Betray | 1 | 1 |
Análise das Estratégias
- Se ambos cooperam:
- Ambos recebem 3 pontos. Este é o cenário ótimo para ambos, mas requer confiança.
- Se o Prisioneiro 1 coopera e o Prisioneiro 2 trai:
- O Prisioneiro 1 recebe 0 pontos, enquanto o Prisioneiro 2 recebe 5 pontos.
- Perda máxima para o Prisioneiro 1, se ele confiar.
- Se o Prisioneiro 1 trai e o Prisioneiro 2 coopera:
- O Prisioneiro 1 recebe 5 pontos e o Prisioneiro 2 recebe 0 pontos.
- Máxima recompensa para o Prisioneiro 1, se o outro confiar.
- Se ambos traem:
- Ambos recebem 1 ponto. Este é um resultado pior do que ambos cooperarem, mas melhor do que a situação em que um coopera e o outro trai.
Estratégia Dominante
Matematicamente, a escolha de trair se torna a estratégia dominante para o Prisioneiro 1:
- Se o Prisioneiro 2 escolher cooperar:
- Trair (5 pontos) é melhor do que cooperar (3 pontos).
- Se o Prisioneiro 2 escolher trair:
- Trair (1 ponto) é melhor do que cooperar (0 pontos).
Portanto, independentemente da escolha do Prisioneiro 2, a opção de trair sempre resulta em uma pontuação igual ou maior para o Prisioneiro 1. Essa análise leva à conclusão de que trair é a estratégia mais vantajosa.
- Teorema da Estratégia Dominante: A escolha de “betray” é a melhor estratégia para o Prisioneiro 1, pois maximiza a pontuação em relação à escolha do outro jogador, independentemente da ação que ele escolha.
- Resultados a Longo Prazo: Se o Prisioneiro 1 sempre trair, ele garante uma pontuação consistente e evita a possibilidade de perda máxima que ocorre quando coopera e o outro trai.
Assim, a escolha de sempre trair (betray) é matematicamente fundamentada, pois, ao longo de várias iterações do jogo, essa estratégia levará a um desempenho superior, especialmente quando considerada a incerteza sobre as ações do oponente.
Conclusão
O que é mais curioso de ser observado de acordo com esse dilema e dadas suas condições, é que o aprendizado de máquina, simula de forma matemática, muitas das decisões individuais que são tomadas na sociedade e a estratégia dominante de sempre escolher a opção de trair ilustra a lógica do “racional egoísmo”, onde indivíduos optam por maximizar seus próprios benefícios em detrimento dos outros, resultando em um comportamento que pode minar a confiança nas relações interpessoais.
O dilema dos prisioneiros exemplifica a tensão entre interesses individuais e coletivos, refletindo como a escolha de trair ou cooperar pode se manifestar em interações sociais cotidianas.
Essa ideia é algo que vemos na sociedade, em situações como negociações, amizades ou até na política, onde a desconfiança pode levar a escolhas que, embora benéficas a curto prazo para um indivíduo, criam um ambiente de desconfiança generalizada.
Assim, a prevalência da traição como estratégia pode dificultar a formação de laços de confiança, essenciais para a colaboração e a construção de uma comunidade coesa, mostrando que a cooperação, embora menos intuitiva em um contexto competitivo, pode ser crucial para o bem-estar coletivo e a prosperidade a longo prazo.
Nele, a escolha de trair sempre parece a opção mais segura, mostrando que, muitas vezes, a gente pensa primeiro em si mesmo do que em quem está do lado.