Este artigo extenso tem o objetivo de cobrir especificamente a parte da teoria e práticas das etapas de construção de hipóteses e validação estatística de testes A/B. A implementação dos testes e ferramentas necessárias para realização dos testes não serão abordadas.
Se você torturar os dados o suficiente, eles confessarão qualquer coisa.
Ronald H. Coase, um renomado economista britânico.
O teste de hipóteses estatístico é uma ferramenta valiosa para tomar decisões informadas em um ambiente de negócios. Por exemplo, se você está lançando um novo produto e deseja saber se ele é realmente mais popular que o produto anterior, você pode usar um teste de hipóteses para analisar os dados de vendas e determinar se há uma diferença significativa entre os dois. Isso ajuda a tomar decisões estratégicas com base em evidências sólidas.
É uma técnica fundamental na inferência estatística. Ele permite que os pesquisadores avaliem as afirmações com base em dados amostrais e determinem se essas afirmações são estatisticamente significativas. Isso é feito comparando os resultados observados com o que seria esperado ao acaso, usando métodos estatísticos.
Antes de nos aprofundarmos em uma análise completa e detalhada de um teste AB, é crucial realizar uma reflexão. Vamos começar esclarecendo alguns pontos fundamentais:
Testes AB bem projetados são bem-sucedidos em qualquer caso:
Mesmo que o resultado não seja o esperado. O que importa são as aprendizagens; um teste AB bem estruturado nos permite planejar os próximos passos com base nele, novamente, mesmo que o resultado não seja o esperado.
O teste AB funciona como uma ferramenta, não como um obstáculo.
Frequentemente, ouvimos diferentes pessoas reclamando do tempo que os testes AB consomem e como estão atrasando a implementação de mudanças. O problema é que, uma vez que uma nova alteração é implementada, se algo der errado, não conseguimos ter 100% de certeza se é por causa da última mudança ou não.
De fato, mesmo se tudo correr bem, não conseguiremos garantir que isso aconteceu por causa daquela nova alteração. Correlação e causalidade são duas coisas diferentes.
Na teoria, os testes AB giram principalmente em torno das técnicas estatísticas para avaliar diferentes variantes e comprovar ou rejeitar uma hipótese.
No entanto, na vida real, as coisas são um pouco diferentes. De fato, eu diria que em qualquer campo relacionado a dados, um dos principais temas é a limpeza e pré-processamento de dados. Isso é especialmente relevante quando pensamos em como os testes AB reais funcionam.
Por exemplo, aplicar diferentes tratamentos a diferentes usuários em aplicativos móveis ou sites requer o uso de ferramentas especiais, que, embora eficazes, não são infalíveis. Portanto, se não prepararmos os dados levando isso em consideração, quaisquer passos futuros serão prejudicados por erros.
Normalmente, em uma empresa, não teremos todo o tempo que gostaríamos para investigar todas as opções e maneiras diferentes de realizar testes AB.
Além disso, construir um pipeline para automatizar isso leva tempo, se pensarmos agora em adicionar dashboards para que usuários não técnicos e analistas possam analisar os resultados, isso leva ainda mais tempo.
Por causa disso, em muitos casos, eu sugeriria começar com abordagens mais simples. Se realmente não entendermos por que estamos escolhendo uma abordagem mais complexa em vez de uma mais simples, estamos fazendo algo errado.
Como regra básica, a abordagem mais fácil que atende às nossas necessidades é a opção certa.
Testagem A/B
O projeto de experimentos é um dos pilares da prática estatística, com aplicações em praticamente todas as áreas de pesquisa. O objetivo é projetar um experimento a fim de confirmar ou rejeitar uma hipótese.
Os cientistas de dados são confrontados com a necessidade de conduzir experimentos contínuos, especialmente no que diz respeito à interface de usuário e marketing de produto.
Um teste A/B é um experimento com dois grupos para determinar gual dos dois tratamentos, produtos, procedimentos ou semelhantes é o superior. Geralmente, um dos dois tratamentos é o tratamento-padrão existente, ou nenhum tratamento.
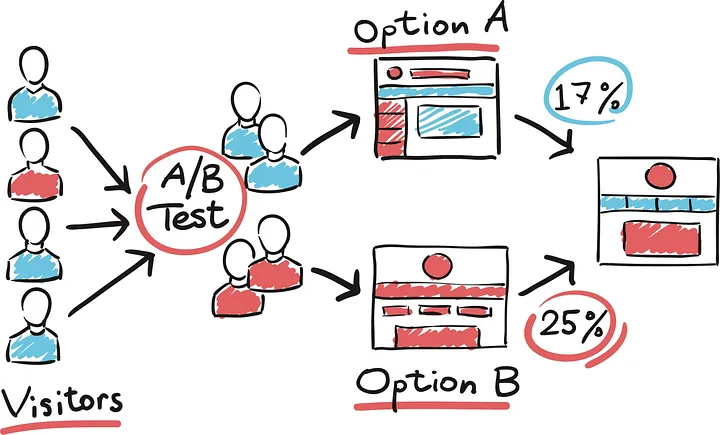
Se um tratamento-padrão (ou nenhum) for usado, este será chamado de controle. A hipótese mais comum utilizada em testes A/B é a de que o tratamento seja melhor que o controle.
Termos-chave para Testagem A/B
- Tratamento: Algo (droga, preço, título de site) ao qual um indivíduo é exposto. (Popularmente conhecido como variação, versão ou hipótese)
- Grupo de tratamento: Um grupo de indivíduos expostos a um tratamento específico.
- Grupo de controle: Um grupo de indivíduos expostos a nenhum tratamento (ou padrão).
- Randomização: O processo de atribuir aleatoriamente indivíduos a tratamentos.
- Individuos: Os itens (visitantes de um site, pacientes etc.) que são expostos aos tratamentos.
- Estatística de teste: A métrica usada para medir o efeito do tratamento.
Um teste A/B adequado tem indivíduos que podem ser atribuídos a um tratamento ou outro. O indivíduo pode ser uma pessoa, uma semente, um visitante de site, e o objetivo é que o indivíduo seja exposto ao tratamento.
O ideal é que os indivíduos sejam randomizados (atribuídos aleatoriamente) aos tratamentos. Dessa forma, sabe-se que qualquer diferença entre os grupos de tratamento é devido a um dos seguintes motivos:
- O efeito de diferentes tratamentos.
- O sorteio no qual os indivíduos são atribuídos a quais tratamentos (ou seja, a atribuição aleatória pode resultar a concentração de indivíduos com melhor desempenho em A ou B).
É necessário também prestar atenção à estatística de teste ou métrica usada para comparar o grupo A ao grupo B. Talvez a métrica mais comum em ciências de dados seja uma variável binária: clicar ou não clicar, comprar ou não comprar, fraude ou não fraude e assim por diante.
O que é uma Hipótese
O processo de experimentos começa com uma hipótese (“a droga A é melhor que a droga-padrão exis-tente”, “o preço A é mais lucrativo que o preço B existente”). O teste (A/B) é um tipo de experimento desenhado para testar a hipótese projetado para trazer resultados conclusivos.
Os dados são coletados e analisados, e então se tira uma conclusão. O termo inferência reflete a intenção de aplicar os resultados do experimento, o que envolve um conjunto limitado de dados, em um processo ou população maiores.

Uma hipótese é uma ideia que você tem sobre alguma coisa com base no que você já sabe. É como fazer uma previsão educada antes de fazer um experimento ou investigação para ver se a sua ideia está correta. As empresas testam essas hipóteses por meio de pesquisas de mercado, feedback dos clientes e análise de dados para tomar decisões informadas sobre seus negócios.
Na estatística, uma hipótese trata-se de uma suposição quanto ao valor de um parâmetro populacional ou quanto à natureza da distribuição de probabilidade de uma variável populacional.
As hipóteses, sempre irão ser construídas em relação à população e nunca para a amostra, pois não faz sentido gerar uma hipótese para a amostra. A amostra sempre será utilizada para gerar o cálculo para provar a hipótese, e nunca o contrário.
Premissas para construção de uma hipótese:
A construção de uma hipótese estatística segue um processo rigoroso e requer algumas premissas fundamentais para que seja considerada válida. Afinal, se você não consegue comprovar estatisticamente de forma válida sua hipótese, suas conclusões serão meramente intuitivas e sem sustento científico, o que prejudica a tomada de decisões acertivas.
As premissas podem variar dependendo do tipo de teste estatístico que está sendo realizado, mas aqui estão as premissas gerais para a construção de uma hipótese estatística:

Variáveis: É importante identificar claramente as variáveis envolvidas na hipótese. Uma variável independente é aquela que é manipulada ou considerada como causa, enquanto uma variável dependente é aquela que é medida ou considerada como resultado.
Teste Estatístico Adequado: Escolher o teste estatístico apropriado com base na natureza das variáveis (por exemplo, teste t para comparação de médias, teste qui-quadrado para associação entre variáveis categóricas, regressão linear para modelagem de relacionamentos etc.).
Distribuição dos Dados: Pressupõe-se que os dados sigam uma distribuição estatística conhecida, geralmente a distribuição normal. Se os dados não atenderem a essa premissa, podem ser necessários ajustes ou testes estatísticos não paramétricos.
Independência das Observações: Cada observação deve ser independente das outras. Isso significa que os dados de uma observação não devem ser influenciados pelos dados de outras observações.
Homogeneidade das Variâncias: Em muitos testes, assume-se que as variâncias nas diferentes categorias ou grupos sendo comparados são aproximadamente iguais. Isso é conhecido como homogeneidade de variâncias.
Tamanho da Amostra Adequado: É importante ter um tamanho de amostra suficientemente grande para que os resultados do teste estatístico sejam confiáveis. O tamanho da amostra depende da natureza dos dados e do poder do teste desejado.
Nível de Significância (α): É necessário escolher um nível de significância antes de realizar o teste. O nível de significância (geralmente definido como 0,05) determina a probabilidade de cometer um erro do Tipo 1 (rejeitar erroneamente a hipótese nula) que será explicado mais a frente.
Poder do Teste (1 – β): O poder do teste é a capacidade do teste de detectar uma diferença ou efeito quando ele realmente existe. Um poder de teste mais alto é desejável.
Plano de Amostragem: Definir claramente como a amostra foi coletada, incluindo o método de seleção e critérios de inclusão/exclusão (por exemplo através de pesquisa online, quais perguntas foram feitas, se as perguntas eram tendenciosas, se a amostra foi selecionada de forma totalmente aleatória dentre outros fatores).
Assunções Específicas: Alguns testes estatísticos podem ter premissas específicas adicionais. Por exemplo, na regressão linear, é importante verificar a multicolinearidade e a normalidade dos resíduos.
Certifique-se de que todas essas premissas sejam atendidas antes de prosseguir com o teste estatístico. Caso contrário, os resultados podem ser comprometidos e as conclusões podem ser inválidas.
Além disso, a construção adequada de hipóteses estatísticas é uma parte fundamental da análise estatística e da pesquisa científica.
Estrutura de uma hipótese
Para formular hipóteses científicas em testes A/B, é necessário seguir alguns princípios:
- Clareza e precisão: A hipótese deve ser clara, concisa e facilmente compreensível. Evite linguagem ambígua ou termos vagos.
- Falsificabilidade: A hipótese deve ser testável e potencialmente refutável. Ou seja, deve ser possível coletar dados que a contradigam ou sustentem.
- Relevância: A hipótese deve ser relevante para o objetivo do teste A/B e para a questão de pesquisa que você está tentando responder.
- Especificidade: A hipótese deve ser específica e quantificável, definindo claramente as variáveis e os resultados esperados.
- Objetividade: A hipótese deve ser neutra e imparcial, evitando viés ou pré-concepções.

Uma boa estrutura para uma hipótese científica em testes A/B pode seguir o seguinte formato:
Se (condição A), então (resultado B).
Por exemplo:
Se (alterarmos o título da página para X), então (a taxa de conversão aumentará em Y%)
Na hipótese “Se (alterarmos o título da página para X), então (a taxa de conversão aumentará em Y%)”, podemos identificar os seguintes elementos:
1. Condição: “Alterarmos o título da página para X“: Essa parte define a condição que será testada. No caso, a variável independente é o título da página, que será alterado para uma nova versão “X”.
2. Resultado: “A taxa de conversão aumentará em Y%“: Essa parte define o resultado esperado da mudança. A variável dependente é a taxa de conversão, que se espera que aumente em uma quantidade específica “Y%” como resultado da alteração do título.
3. Relação causal: A palavra “então” indica uma relação causal entre a condição e o resultado. A hipótese sugere que a mudança no título da página causa um aumento na taxa de conversão.
4. Falsificabilidade: A hipótese é falsificável, pois é possível coletar dados que a contradizem. Se a taxa de conversão não aumentar ou até mesmo diminuir após a mudança do título, a hipótese seria refutada.
5. Especificidade: A hipótese é específica, pois define claramente a variável independente (título da página), a variável dependente (taxa de conversão) e o efeito esperado (aumento de Y%).
6. Objetividade: A hipótese é objetiva, pois não apresenta viés ou pré-concepções sobre o resultado da mudança.
Exemplos de hipóteses científicas para testes A/B:
- Se (alterarmos o título da página para X), então (a taxa de conversão aumentará em Y%).
- Se (personalizarmos o conteúdo da página para cada usuário), então (o tempo médio gasto na página aumentará em Z%).
- Se (removermos o formulário de inscrição), então (a taxa de abandono do carrinho diminuirá em W%).
- Se (oferecermos um desconto de X%), então (as vendas aumentarão em Y%).
- Se (enviarmos um e-mail de acompanhamento após 24 horas), então (a taxa de resposta aumentará em Z%).
Dicas para formular hipóteses:
- Comece com uma pergunta de pesquisa clara e específica.
- Realize uma pesquisa inicial para entender o contexto e as variáveis relevantes.
- Faça brainstorming e gere várias hipóteses possíveis.
- Avalie a viabilidade e a testabilidade de cada hipótese.
- Selecione a hipótese mais relevante e com maior potencial de impacto.
- Refine a hipótese para torná-la clara, específica e quantificável.
Com um processo rigoroso e criterioso, você pode formular hipóteses científicas robustas para seus testes A/B, aumentando as chances de obter resultados válidos e insights valiosos para otimizar suas campanhas e produtos.
Hipótese Nula e Hipótese Alternativa
Para testar um parâmetro amostral, devemos afirmar cuidadosamente um par de hipóteses:
- Uma que represente a realidade atual e nula (H0)
- Outra que represente seu contraponto (Ha)
Quando uma dessas hipóteses for falsa, a outra deve ser verdadeira
Essas duas hipóteses são chamadas de hipótese nula e hipótese alternativa
Em um teste de hipóteses, sempre partimos do pressuposto que a hipótese nula (H0) é verdadeira. Daí podemos tomar duas decisões:
- Aceitar H0 rejeitando Ha
- Aceitar Ha rejeitando H0

Hipótese Nula (H0)
Uma hipótese nula geralmente afirma que não existe relação entre dois fenômenos medidos. Em pesquisa de mercado: “um aumento de 5% no preço de um determinado produto não afetará adversamente as vendas dele”.
Quando não é possível ou viável observar toda a população, o teste é baseado na observação de uma amostra aleatória da população. Tal parâmetro é frequentemente a média ou o desvio padrão.
Se quisermos comparar os resultados nos exames de duas amostras aleatórias de homens e mulheres, a hipótese nula poderia ser “que a média do resultado no exame da população masculina do qual a primeira amostra foi retirada é o mesmo que o da amostra de população feminina, da segunda amostra”:
em que:
- H0 = a hipótese nula
- μ1 = a média da população 1, e
- μ2 = a média da população 2.
Alternativamente, a hipótese nula pode postular que as duas amostras são retiradas da mesma população:
Ou seja, a hipótese nula significa que não houve nenhuma diferença entre a amostra de controle e a variação.
A hipótese nula representa a situação padrão, o status quo que você assume ser verdadeiro. A hipótese alternativa é a que você quer confirmar como verdadeira.
Por exemplo, se você está testando uma nova estratégia de marketing, a hipótese nula pode ser que a estratégia antiga é tão eficaz quanto a nova, e a hipótese alternativa é que a nova estratégia é melhor.
Você coleta dados para ver se pode rejeitar a hipótese nula e adotar a nova estratégia com confiança.
Em estatísticas, a hipótese nula (H0) é uma afirmação que assume que não há efeito ou diferença significativa em um conjunto de dados.
Hipótese Alternativa (Ha)
A hipótese alternativa em um contexto de negócios é uma suposição que uma empresa faz ao lançar um novo produto, serviço ou estratégia. Ela representa a ideia de que essa nova abordagem será bem-sucedida e levará a resultados positivos.
Ao coletar dados e realizar análises, a empresa tenta determinar se a hipótese alternativa é válida e se a nova iniciativa é realmente eficaz. Em resumo, a hipótese alternativa é a aposta de que uma mudança ou ação terá um impacto positivo nos negócios.

Na estatística, a hipótese alternativa é uma declaração que desafia a hipótese nula (H0) em um teste de hipóteses. Ela é formulada com base na suposição de que há um efeito, diferença, associação ou relação estatisticamente significativa entre as variáveis em estudo.
Em outras palavras, a hipótese alternativa (geralmente denotada como H1 ou Ha) é a hipótese que um pesquisador ou analista deseja testar e provar. Ela representa a ideia de que há algo acontecendo nos dados que não é devido ao acaso ou ao erro amostral.
A hipótese alternativa é crucial porque direciona o teste estatístico e as análises subsequentes. O objetivo é coletar evidências dos dados que apoiem a hipótese alternativa e refutem a hipótese nula. Isso é feito calculando uma estatística de teste apropriada e comparando-a com um valor crítico ou calculando um valor p para determinar se as diferenças observadas são estatisticamente significativas.
Ela sugere que há uma relação ou efeito de interesse nas variáveis estudadas e é usada para determinar se os resultados dos dados são estatisticamente convincentes o suficiente para rejeitar a hipótese nula.
Distribuição Normal e o Teorema do Limite Central
A curva normal é como uma montanha suave e simétrica, alta no meio e descendo devagar para os lados.
O teorema do limite central diz que, se você fizer muitas vezes uma mesma coisa e medir os resultados, eles sempre formarão uma montanha como essa, mesmo que os resultados individuais sejam diferentes.
A curva normal e o Teorema do Limite Central são conceitos fundamentais em estatística e probabilidade, com aplicações extensivas em diversas áreas, incluindo ciências sociais, finanças, engenharia e ciências naturais.
Estes conceitos ajudam a entender e analisar distribuições de dados e comportamentos aleatórios em populações grandes pois são ferramentas essenciais na análise e interpretação de dados.
O que é a Distribuição Normal (Gaussiana)?
A Distribuição Normal (Gaussiana) proporciona uma maneira simplificada de representar dados reais
A curva normal, também conhecida como distribuição normal ou distribuição de Gauss, é uma distribuição de probabilidade contínua que é simétrica em torno da sua média.

Essa distribuição tem um formato característico de “sino”, com a maioria dos valores concentrados em torno da média e caindo gradualmente nas extremidades.
A curva normal, ou distribuição normal, é uma função de densidade de probabilidade simétrica em torno da média, representada por uma “curva em forma de sino”.
Características da Curva Normal
- Média, Mediana e Moda Iguais: Na distribuição normal, a média, mediana e moda são todas iguais e localizadas no centro da distribuição.
- Simetria: A curva é perfeitamente simétrica em torno da média.
- Assimptótica: As caudas da curva se aproximam do eixo horizontal, mas nunca tocam nele.
- Desvio Padrão: O desvio padrão determina a largura da curva; aproximadamente 68% dos dados caem dentro de um desvio padrão da média, 95% dentro de dois desvios padrões, e 99,7% dentro de três desvios padrões.
O que é o Teorema do Limite Central?
O teorema do limite central afirma que, conforme o tamanho da amostra aumenta, a distribuição da média das amostras tende a uma distribuição normal, independentemente da forma da distribuição original da população.
O Teorema Central do Limite (TCL) é um resultado crucial na estatística, sendo a base para a demonstração de vários outros teoremas estatísticos.

Na teoria das probabilidades, este teorema indica que, conforme o tamanho da amostra aumenta, a distribuição das médias amostrais se aproxima de uma distribuição normal. Esse princípio é essencial na teoria da inferência estatística.
Na inferência estatística, o TCL é útil para estimar parâmetros como a média populacional e o desvio padrão a partir de uma amostra aleatória.
Isso significa que, com base na média e no desvio padrão da amostra, é possível calcular a probabilidade de um parâmetro ocorrer dentro de um determinado intervalo.
O Teorema Central do Limite é um dos conceitos mais significativos na teoria das probabilidades. Ele estabelece que, sob determinadas condições, a soma (ou média) de um grande número de variáveis aleatórias independentes e identicamente distribuídas tende a seguir uma distribuição normal, independentemente da distribuição original dessas variáveis.
Distribuição Normal em Testes A/B
Em um teste A/B, os dados coletados (como taxas de conversão, cliques, etc.) muitas vezes seguem uma distribuição que pode ser aproximada por uma distribuição normal.
Isso ocorre porque, em muitos casos, os fatores que influenciam o comportamento dos usuários são numerosos e independentes, resultando em uma soma de variáveis aleatórias que tende a uma distribuição normal, conforme indicado pelo Teorema do Limite Central.
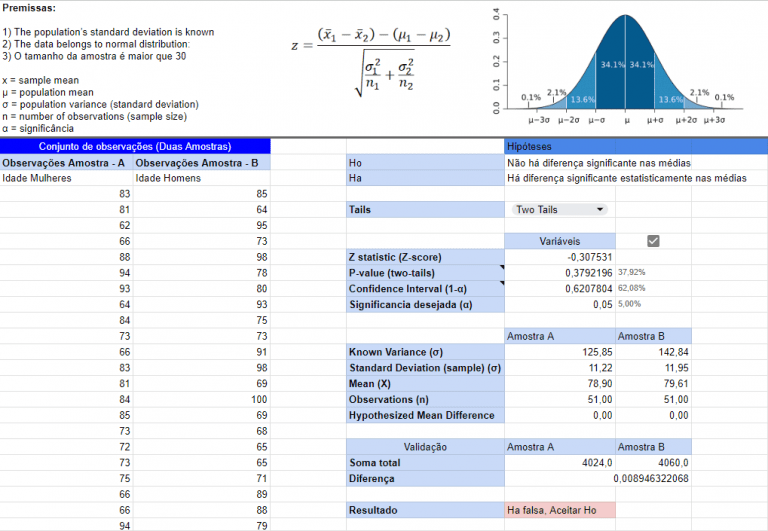
Exemplo de simulação de testagem bicaudal e 95% de confiança utilizando os seguintes parâmetros:


Importância do Teorema do Limite Central
- Aproximação de Distribuições: Permite que distribuições de amostras grandes sejam aproximadas por uma distribuição normal, facilitando cálculos e inferências estatísticas.
- Inferência Estatística: Baseia muitas técnicas de inferência estatística, incluindo intervalos de confiança e testes de hipóteses.
- Robustez: Aplica-se a uma ampla gama de distribuições diferentes, desde que tenham média e variância finitas.
Simulando na prática a distribuição de dados:
Esta simulação permite explorar vários aspectos das distribuições amostrais. Quando a simulação começa, um histograma de uma distribuição normal é exibido na parte superior da tela.
A distribuição retratada na parte superior da tela é a população da qual as amostras são retiradas. A média da distribuição é indicada por uma pequena linha azul e a mediana é indicada por uma pequena linha roxa. Como a média e a mediana são iguais, as duas linhas se sobrepõem.
A linha vermelha se estende da média em uma direção de um desvio padrão para cada lado. Observe a correspondência entre as cores usadas no histograma e as estatísticas exibidas à esquerda do histograma.
O segundo histograma exibe os dados da amostra. Este histograma está inicialmente em branco. O terceiro e o quarto histogramas mostram a distribuição das estatísticas calculadas a partir dos dados da amostra.
O número de amostras (replicações) que os terceiro e quarto histogramas são baseados é indicado pelo rótulo “Reps=.”
Estado inicial com 5 Reps:

Estado inicial com 10.007 Reps:

Aplicações Práticas
Na Pesquisa Científica, pesquisadores frequentemente utilizam o Teorema do Limite Central para justificar o uso de métodos de inferência baseados na distribuição normal, mesmo quando a distribuição original dos dados não é normal.
Na Engenharia, engenheiros utilizam a curva normal para modelar erros e ruídos em sistemas, assumindo que muitos pequenos efeitos aleatórios se combinam para produzir um comportamento normalmente distribuído.
Na Economia e Finanças, economistas e analistas financeiros aplicam a distribuição normal para modelar retornos de ativos financeiros e para prever comportamentos de mercado, utilizando a suposição de que fatores de mercado independentes afetam os preços de maneira acumulativa.
Significância Estatística e Valores P
Em estatísticas, a significância estatística refere-se à probabilidade de que os resultados de um estudo ou experimento não são devidos ao acaso. Geralmente, é representada por um valor de p.
Se o valor de p for menor que um limite como 0,05 (que é o nosso alpha), os resultados são considerados estatisticamente significativos. Isso sugere que a diferença observada ou o efeito é provavelmente real e não simplesmente um acaso estatístico. Se o resultado estiver além do domínio da variação do acaso, é chamado de estatisticamente significante.
O Valor P (P-value)
Uma vez que entendemos o que é significância estatística, como vamos medi-la? A simples observação de um gráfico não é uma maneira muito precisa de medir a significância estatística. O valor de P é o número que olhamos para compreender a significância estatística de um Teste, o que torna essa validação mais fácil e interessante.

Alpha
Em experimentos A/B, o “alpha” é o nível de significância que usamos para avaliar a diferença entre as variantes A e B. Os típicos niveis de alfa são 5% e 1%. É como uma regra que decidimos antes de começar a testar coisas.
Os estatísticos não gostam da ideia de deixar a definição de um resultado como “muito incomum” para acontecer por acaso a critério dos pesquisadores. Em vez disso, especifica-se com antecedência um limiar, como em “mais extremo que 5% do resultado do acaso (hipótese nula)”. Esse limiar é conhecido como alpha.
Qualquer nível escolhido é uma escolha arbitrária a critério de quem está construindo o teste, o que significa que há 5% de chance de observarmos uma diferença quando não há realmente nenhuma. É uma medida crítica para controlar erros ao tirar conclusões de experimentos.

Não há nada no processo que garante decisões corretas x% do tempo. Isso acontece porque a questão de probabilidade não é respondida com “qual a probabilidade de isso ter acontecido por acaso?” mas, sim, “dado um modelo de acaso, qual é a probabilidade de haver um resultado tão extremo?”
O Poder do Teste (Observed Power) e o Tamanho da Amostra (Sample Size)
Um alto poder do teste significa que você está mais propenso a identificar padrões, tendências ou relações importantes em seus dados, o que é crucial para tomar decisões de negócios informadas e bem-sucedidas. Em resumo, quanto maior o poder do teste, mais confiável é a análise estatística.
Tamanho do efeito: O tamanho mínimo do efeito que se espera poder detectar em um teste estatístico, por exemplo, “uma melhora de 20% em taxas de clique”.
Poder: A probabilidade de detectar um dado tamanho de efeito com dado tamanho de amostra.
O poder é a probabilidade de detectar um tamanho de efeito especificado com características de amostra especificadas (tamanho e variabilidade).

É um conceito crucial em estatística e testes de hipóteses. Ele representa a probabilidade de rejeitar corretamente a hipótese nula quando ela é, de fato, falsa. Em outras palavras, é a probabilidade de encontrar um efeito significativo se esse efeito realmente existir nos dados.
Ele também pode ser entendido como a probabilidade a longo prazo de obter resultados significativos em uma série de estudos de replicação exata. Por exemplo, um poder de 50% significa que um conjunto de 100 estudos é esperado para produzir 50 resultados significativos e 50 resultados não significativos.
Os números exatos em um conjunto real de estudos variarão devido ao erro de amostragem aleatória, da mesma forma que 100 lançamentos de moedas nem sempre produzirão uma divisão de 50:50 entre caras e coroas. No entanto, à medida que o número de estudos aumenta, a porcentagem de resultados significativos se aproximará cada vez mais do poder de um estudo específico.
Relação com o Erro Tipo II:
O poder do teste está inversamente relacionado ao Erro Tipo II (β). Quanto maior o poder do teste, menores são as chances de cometer um erro do Tipo II, que ocorre quando você não rejeita a hipótese nula quando deveria.
Existem várias maneiras de interpretar o poder do teste:
- O poder é a probabilidade de rejeitar a hipótese nula quando, na verdade, ela é falsa.
- O poder é a probabilidade de tomar uma decisão correta (rejeitar a hipótese nula) quando a hipótese nula é falsa.
- O poder é a probabilidade de um teste de significância detectar um efeito que está presente.
- O poder é a probabilidade de um teste de significância detectar uma discrepância em relação à hipótese nula, caso tal discrepância exista.
- O poder é a probabilidade de evitar um erro do Tipo II.

Aumentando o Poder do Teste:
É importante observar que falamos sobre o poder (power) do teste de hipóteses quando a hipótese alternativa (Ha) é verdadeira. Se, infelizmente, a hipótese nula (H0) for verdadeira e não houver nenhum efeito real, nenhum grau de poder vai nos ajudar. Como pode ser visto no gráfico, quando H0 é verdadeira, lidamos apenas com o erro do tipo I (alpha).
No entanto, na vida real, não temos ideia se H0 ou Ha é verdadeira, e não podemos alterar a verdade fundamental. Tudo o que podemos controlar é a decisão de rejeitar ou não rejeitar H0, com a esperança de que Ha seja verdadeira. Apesar disso, ainda queremos aumentar nosso poder estatístico, para que tenhamos a melhor chance de detectar um efeito real quando ele de fato existe.
No entanto, o poder não pode fazer nada se H0 for verdadeira e não houver efeito real para ser detectado. Portanto, o aumento do poder é uma estratégia para melhorar nossas chances de encontrar um efeito quando ele está presente, mesmo que não possamos garantir a verdade das hipóteses.
Você pode aumentar o poder do teste aumentando o tamanho da amostra, usando testes mais sensíveis ou refinando a forma como você conduz seu experimento.
Tamanho da Amostra (Sample Size)
Pelo tamanho da amostra, entendemos um grupo de indivíduos selecionados da população em geral e considerado representativo da verdadeira população para aquele estudo específico.
Por exemplo, se quisermos prever como a população em um grupo etário específico reagirá a um novo produto, podemos primeiro testá-lo em um tamanho de amostra que seja representativo da população-alvo. O tamanho da amostra, neste caso, será dado pelo número de pessoas nesse grupo etário que serão pesquisadas.
Em testes A/B, o tamanho da amostra é crítico para a confiabilidade dos resultados. Quanto maior a amostra, mais confiáveis são as conclusões tiradas do experimento. Isso está diretamente relacionado ao poder do teste, que é a probabilidade de detectar uma diferença real quando ela existe. Um tamanho de amostra maior geralmente aumenta o poder do teste.

Um dos passos nos cálculos estatísticos para tamanho de amostra é perguntar: “Um teste de hipótese revelará realmente uma diferença entre os tratamentos A e B?” O resultado de um teste de hipótese (o valor p) depende da real diferença entre os tratamentos A e B.
Depende também da sorte na extração, ou seja, quem é selecionado para os grupos no experimento. Mas faz sentido que quanto maior a diferença real entre os tratamentos A e B, maior a probabilidade de que o experimento a revelará. E quanto menor a diferença, mais dados serão necessários para detectá-la.
O uso mais comum dos cálculos de potência é estimar quão grande será a amostra necessária. Por exemplo, suponha que estejamos observando taxas de clique e testando um novo anúncio contra um anúncio existente. Quantos cliques serão necessários no experimento?
Se estivermos interessados apenas em resultados que mostrem uma enorme diferença (digamos, uma diferença de 50%), uma amostra relativamente pequena poderia ser útil. Se, por outro lado, estamos tentando analisar qualquer diferença por menor que seja, então é necessário ter uma amostra muito maior.
Uma abordagem padrão é estabelecer uma política de que um novo anúncio tem que ser melhor que o existente em certo percentual, digamos 10%, ou então o anúncio existente continuará ativo.
Este objetivo, o “tamanho do efeito”, define o tamanho da amostra. Por exemplo, suponhamos que as taxas de clique atuais sejam de cerca de 1,1%, e estamos buscando um aumento de 10% para 1,21%. Então, temos duas caixas: caixa A com 1,1% de uns (digamos, 110 uns e 9.890 zeros), e caixa B com 1,21% de uns (digamos, 121 uns e 9.879 zeros). Para começar, façamos 300 extrações de cada caixa (isso seria como 300 “impressões” para cada anúncio).
Executando o teste de Hipótese
O primeiro passo no teste de hipóteses é calcular a estatística do teste. A fórmula para a estatística do teste depende de se o desvio padrão da população (σ) é conhecido ou desconhecido.
Teste Z ou Teste T?
Se σ for conhecido, nosso teste de hipóteses é conhecido como teste z e usamos a distribuição z. Se σ for desconhecido, nosso teste de hipóteses é conhecido como teste t e usamos a distribuição t. O uso da distribuição t depende dos graus de liberdade, que é igual ao tamanho da amostra menos um.

Além disso, se o desvio padrão da população σ for desconhecido, o desvio padrão da amostra s é usado em seu lugar. Para alternar de σ conhecido para σ desconhecido, você pode utilizar uma calculadora de teste de hipóteses e selecionar a opção apropriada.
Em resumo, a escolha entre o teste z e o teste t depende de se o desvio padrão da população é conhecido e envolve o uso da distribuição correspondente (z ou t) para calcular a estatística do teste.
Se o desvio padrão da população não for conhecido, o desvio padrão da amostra e os graus de liberdade desempenham um papel importante no cálculo da estatística do teste.

Teste Z (Z-test)
O teste Z, também conhecido como Teste Z de uma amostra, é uma técnica estatística usada para avaliar se a média de uma amostra é estatisticamente significativamente diferente da média populacional conhecida ou da média de uma população de referência. O teste Z é particularmente útil quando a variância populacional é conhecida.
Premissas do Teste Z
Para realizar um teste Z, é necessário que as seguintes premissas sejam atendidas:
Variância Populacional Conhecida ou Grande Tamanho da Amostra: A principal premissa é que você conhece a variância populacional (σ²) ou tem um tamanho de amostra (n) suficientemente grande. Um tamanho de amostra grande é geralmente definido como n > 30, embora essa regra possa variar dependendo do contexto.
Independência das Observações: Cada observação na amostra deve ser independente das outras. Isso significa que o valor de uma observação não deve ser afetado pelo valor de outra observação.
Distribuição Normal ou Amostra Grande: Se a variância populacional é conhecida e o tamanho da amostra não é grande (n ≤ 30), é importante que os dados sigam uma distribuição normal. Se o tamanho da amostra for grande, os dados podem não precisar seguir rigorosamente a distribuição normal devido ao Teorema do Limite Central.
Fórmula do Teste Z:
A estatística do teste Z é calculada usando a seguinte fórmula:

- ( Z ) é a estatística do teste Z.
- ( X ) é a média da amostra.
- ( μ ) é a média populacional (ou média de referência).
- ( σ ) é o desvio padrão populacional.
- ( n ) é o tamanho da amostra.
Tabela Z (Z-table)
A tabela Z, também conhecida como Z-table ou Tabela de Distribuição Normal Padrão, é uma ferramenta fundamental em estatística usada para encontrar probabilidades associadas a uma distribuição normal padrão. A distribuição normal padrão é uma distribuição com média zero (μ = 0) e desvio padrão um (σ = 1).
A tabela Z é usada principalmente em conjunto com o teste Z (ou Teste Z) e outros testes estatísticos que envolvem a distribuição normal padrão. Ela permite que os pesquisadores e analistas encontrem rapidamente a probabilidade associada a um valor de Z específico.
A tabela Z é organizada de forma que as probabilidades são fornecidas para diferentes valores de Z, que correspondem aos desvios padrão acima ou abaixo da média da distribuição normal padrão. A tabela mostra a área sob a curva normal à esquerda de um determinado valor de Z.
Para acessar a tabela existe uma versão em https://www.z-table.com/ ou você pode observá-la abaixo:
Tabela Z com valores positivos:
| Z | ,00 | ,01 | ,02 | ,03 | ,04 | ,05 | ,06 | ,07 | ,08 | ,09 |
| 0,0 | 0,5000 | 0,5040 | 0,5080 | 0,5120 | 0,5160 | 0,5199 | 0,5239 | 0,5279 | 0,5319 | 0,5359 |
| 0,1 | 0,5398 | 0,5438 | 0,5478 | 0,5517 | 0,5557 | 0,5596 | 0,5636 | 0,5675 | 0,5714 | 0,5754 |
| 0,2 | 0,5793 | 0,5832 | 0,5871 | 0,5910 | 0,5948 | 0,5987 | 0,6026 | 0,6064 | 0,6103 | 0,6141 |
| 0,3 | 0,6179 | 0,6217 | 0,6255 | 0,6293 | 0,6331 | 0,6368 | 0,6406 | 0,6443 | 0,6480 | 0,6517 |
| 0,4 | 0,6554 | 0,6591 | 0,6628 | 0,6664 | 0,6700 | 0,6736 | 0,6772 | 0,6808 | 0,6844 | 0,6879 |
| 0,5 | 0,6915 | 0,6950 | 0,6985 | 0,7019 | 0,7054 | 0,7088 | 0,7123 | 0,7157 | 0,7190 | 0,7224 |
| 0,6 | 0,7258 | 0,7291 | 0,7324 | 0,7357 | 0,7389 | 0,7422 | 0,7454 | 0,7486 | 0,7518 | 0,7549 |
| 0,7 | 0,7580 | 0,7612 | 0,7642 | 0,7673 | 0,7704 | 0,7734 | 0,7764 | 0,7794 | 0,7823 | 0,7852 |
| 0,8 | 0,7881 | 0,7910 | 0,7939 | 0,7967 | 0,7996 | 0,8023 | 0,8051 | 0,8079 | 0,8106 | 0,8133 |
| 0,9 | 0,8159 | 0,8186 | 0,8212 | 0,8238 | 0,8264 | 0,8289 | 0,8315 | 0,8340 | 0,8365 | 0,8389 |
| 1,0 | 0,8413 | 0,8438 | 0,8461 | 0,8485 | 0,8508 | 0,8531 | 0,8554 | 0,8577 | 0,8599 | 0,8621 |
| 1,1 | 0,8643 | 0,8665 | 0,8686 | 0,8708 | 0,8729 | 0,8749 | 0,8770 | 0,8790 | 0,8810 | 0,8830 |
| 1,2 | 0,8849 | 0,8869 | 0,8888 | 0,8907 | 0,8925 | 0,8944 | 0,8962 | 0,8980 | 0,8997 | 0,9015 |
| 1,3 | 0,9032 | 0,9049 | 0,9066 | 0,9082 | 0,9099 | 0,9115 | 0,9131 | 0,9147 | 0,9162 | 0,9177 |
| 1,4 | 0,9192 | 0,9207 | 0,9222 | 0,9236 | 0,9251 | 0,9265 | 0,9279 | 0,9292 | 0,9306 | 0,9319 |
| 1,5 | 0,9332 | 0,9345 | 0,9357 | 0,9370 | 0,9382 | 0,9394 | 0,9406 | 0,9418 | 0,9430 | 0,9441 |
| 1,6 | 0,9452 | 0,9463 | 0,9474 | 0,9485 | 0,9495 | 0,9505 | 0,9515 | 0,9525 | 0,9535 | 0,9545 |
| 1,7 | 0,9554 | 0,9564 | 0,9573 | 0,9582 | 0,9591 | 0,9599 | 0,9608 | 0,9616 | 0,9625 | 0,9633 |
| 1,8 | 0,9641 | 0,9649 | 0,9656 | 0,9664 | 0,9671 | 0,9678 | 0,9686 | 0,9693 | 0,9700 | 0,9706 |
| 1,9 | 0,9713 | 0,9719 | 0,9726 | 0,9732 | 0,9738 | 0,9744 | 0,9750 | 0,9756 | 0,9762 | 0,9767 |
| 2,0 | 0,9773 | 0,9778 | 0,9783 | 0,9788 | 0,9793 | 0,9798 | 0,9803 | 0,9808 | 0,9812 | 0,9817 |
| 2,1 | 0,9821 | 0,9826 | 0,9830 | 0,9834 | 0,9838 | 0,9842 | 0,9846 | 0,9850 | 0,9854 | 0,9857 |
| 2,2 | 0,9861 | 0,9865 | 0,9868 | 0,9871 | 0,9875 | 0,9878 | 0,9881 | 0,9884 | 0,9887 | 0,9890 |
| 2,3 | 0,9893 | 0,9896 | 0,9898 | 0,9901 | 0,9904 | 0,9906 | 0,9909 | 0,9911 | 0,9913 | 0,9916 |
| 2,4 | 0,9918 | 0,9920 | 0,9922 | 0,9925 | 0,9927 | 0,9929 | 0,9931 | 0,9932 | 0,9934 | 0,9936 |
| 2,5 | 0,9938 | 0,9940 | 0,9941 | 0,9943 | 0,9945 | 0,9946 | 0,9948 | 0,9949 | 0,9951 | 0,9952 |
| 2,6 | 0,9953 | 0,9955 | 0,9956 | 0,9957 | 0,9959 | 0,9960 | 0,9961 | 0,9962 | 0,9963 | 0,9964 |
| 2,7 | 0,9965 | 0,9966 | 0,9967 | 0,9968 | 0,9969 | 0,9970 | 0,9971 | 0,9972 | 0,9973 | 0,9974 |
| 2,8 | 0,9974 | 0,9975 | 0,9976 | 0,9977 | 0,9977 | 0,9978 | 0,9979 | 0,9980 | 0,9980 | 0,9981 |
| 2,9 | 0,9981 | 0,9982 | 0,9983 | 0,9983 | 0,9984 | 0,9984 | 0,9985 | 0,9985 | 0,9986 | 0,9986 |
| 3,0 | 0,9987 | 0,9987 | 0,9987 | 0,9988 | 0,9988 | 0,9989 | 0,9989 | 0,9989 | 0,9990 | 0,9990 |
| 3,1 | 0,9990 | 0,9991 | 0,9991 | 0,9991 | 0,9992 | 0,9992 | 0,9992 | 0,9992 | 0,9993 | 0,9993 |
| 3,2 | 0,9993 | 0,9993 | 0,9994 | 0,9994 | 0,9994 | 0,9994 | 0,9994 | 0,9995 | 0,9995 | 0,9995 |
| 3,3 | 0,9995 | 0,9995 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9997 |
| 3,4 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9998 | 0,9998 |
| 3,5 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 |
| 3,6 | 0,9998 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 |
| 3,7 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 |
| 3,8 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 1,0000 | 1,0000 | 1,0000 |
| 3,9 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |

Tabela Z com valores negativos:
| Z | ,00 | ,01 | ,02 | ,03 | ,04 | ,05 | ,06 | ,07 | ,08 | ,09 |
| -3,9 | 0,00005 | 0,00005 | 0,00004 | 0,00004 | 0,00004 | 0,00004 | 0,00004 | 0,00004 | 0,00003 | 0,00003 |
| -3,8 | 0,00007 | 0,00007 | 0,00007 | 0,00006 | 0,00006 | 0,00006 | 0,00006 | 0,00005 | 0,00005 | 0,00005 |
| -3,7 | 0,00011 | 0,00010 | 0,00010 | 0,00010 | 0,00009 | 0,00009 | 0,00008 | 0,00008 | 0,00008 | 0,00008 |
| -3,6 | 0,00016 | 0,00015 | 0,00015 | 0,00014 | 0,00014 | 0,00013 | 0,00013 | 0,00012 | 0,00012 | 0,00011 |
| -3,5 | 0,00023 | 0,00022 | 0,00022 | 0,00021 | 0,00020 | 0,00019 | 0,00019 | 0,00018 | 0,00017 | 0,00017 |
| -3,4 | 0,00034 | 0,00032 | 0,00031 | 0,00030 | 0,00029 | 0,00028 | 0,00027 | 0,00026 | 0,00025 | 0,00024 |
| -3,3 | 0,00048 | 0,00047 | 0,00045 | 0,00043 | 0,00042 | 0,00040 | 0,00039 | 0,00038 | 0,00036 | 0,00035 |
| -3,2 | 0,00069 | 0,00066 | 0,00064 | 0,00062 | 0,00060 | 0,00058 | 0,00056 | 0,00054 | 0,00052 | 0,00050 |
| -3,1 | 0,00097 | 0,00094 | 0,00090 | 0,00087 | 0,00084 | 0,00082 | 0,00079 | 0,00076 | 0,00074 | 0,00071 |
| -3,0 | 0,00135 | 0,00131 | 0,00126 | 0,00122 | 0,00118 | 0,00114 | 0,00111 | 0,00107 | 0,00104 | 0,00100 |
| -2,9 | 0,00187 | 0,00181 | 0,00175 | 0,00169 | 0,00164 | 0,00159 | 0,00154 | 0,00149 | 0,00144 | 0,00139 |
| -2,8 | 0,00256 | 0,00248 | 0,00240 | 0,00233 | 0,00226 | 0,00219 | 0,00212 | 0,00205 | 0,00199 | 0,00193 |
| -2,7 | 0,00347 | 0,00336 | 0,00326 | 0,00317 | 0,00307 | 0,00298 | 0,00289 | 0,00280 | 0,00272 | 0,00264 |
| -2,6 | 0,00466 | 0,00453 | 0,00440 | 0,00427 | 0,00415 | 0,00402 | 0,00391 | 0,00379 | 0,00368 | 0,00357 |
| -2,5 | 0,00621 | 0,00604 | 0,00587 | 0,00570 | 0,00554 | 0,00539 | 0,00523 | 0,00508 | 0,00494 | 0,00480 |
| -2,4 | 0,00820 | 0,00798 | 0,00776 | 0,00755 | 0,00734 | 0,00714 | 0,00695 | 0,00676 | 0,00657 | 0,00639 |
| -2,3 | 0,01072 | 0,01044 | 0,01017 | 0,00990 | 0,00964 | 0,00939 | 0,00914 | 0,00889 | 0,00866 | 0,00842 |
| -2,2 | 0,01390 | 0,01355 | 0,01321 | 0,01287 | 0,01255 | 0,01222 | 0,01191 | 0,01160 | 0,01130 | 0,01101 |
| -2,1 | 0,01786 | 0,01743 | 0,01700 | 0,01659 | 0,01618 | 0,01578 | 0,01539 | 0,01500 | 0,01463 | 0,01426 |
| -2,0 | 0,02275 | 0,02222 | 0,02169 | 0,02118 | 0,02068 | 0,02018 | 0,01970 | 0,01923 | 0,01876 | 0,01831 |
| -1,9 | 0,02872 | 0,02807 | 0,02743 | 0,02680 | 0,02619 | 0,02559 | 0,02500 | 0,02442 | 0,02385 | 0,02330 |
| -1,8 | 0,03593 | 0,03515 | 0,03438 | 0,03362 | 0,03288 | 0,03216 | 0,03144 | 0,03074 | 0,03005 | 0,02938 |
| -1,7 | 0,04457 | 0,04363 | 0,04272 | 0,04182 | 0,04093 | 0,04006 | 0,03920 | 0,03836 | 0,03754 | 0,03673 |
| -1,6 | 0,05480 | 0,05370 | 0,05262 | 0,05155 | 0,05050 | 0,04947 | 0,04846 | 0,04746 | 0,04648 | 0,04551 |
| -1,5 | 0,06681 | 0,06552 | 0,06426 | 0,06301 | 0,06178 | 0,06057 | 0,05938 | 0,05821 | 0,05705 | 0,05592 |
| -1,4 | 0,08076 | 0,07927 | 0,07780 | 0,07636 | 0,07493 | 0,07353 | 0,07215 | 0,07078 | 0,06944 | 0,06811 |
| -1,3 | 0,09680 | 0,09510 | 0,09342 | 0,09176 | 0,09012 | 0,08851 | 0,08691 | 0,08534 | 0,08379 | 0,08226 |
| -1,2 | 0,11507 | 0,11314 | 0,11123 | 0,10935 | 0,10749 | 0,10565 | 0,10383 | 0,10204 | 0,10027 | 0,09853 |
| -1,1 | 0,13567 | 0,13350 | 0,13136 | 0,12924 | 0,12714 | 0,12507 | 0,12302 | 0,12100 | 0,11900 | 0,11702 |
| -1,0 | 0,15866 | 0,15625 | 0,15386 | 0,15151 | 0,14917 | 0,14686 | 0,14457 | 0,14231 | 0,14007 | 0,13786 |
| -0,9 | 0,18406 | 0,18141 | 0,17879 | 0,17619 | 0,17361 | 0,17106 | 0,16853 | 0,16602 | 0,16354 | 0,16109 |
| -0,8 | 0,21186 | 0,20897 | 0,20611 | 0,20327 | 0,20045 | 0,19766 | 0,19489 | 0,19215 | 0,18943 | 0,18673 |
| -0,7 | 0,24196 | 0,23885 | 0,23576 | 0,23270 | 0,22965 | 0,22663 | 0,22363 | 0,22065 | 0,21770 | 0,21476 |
| -0,6 | 0,27425 | 0,27093 | 0,26763 | 0,26435 | 0,26109 | 0,25785 | 0,25463 | 0,25143 | 0,24825 | 0,24510 |
| -0,5 | 0,30854 | 0,30503 | 0,30153 | 0,29806 | 0,29460 | 0,29116 | 0,28774 | 0,28434 | 0,28096 | 0,27760 |
| -0,4 | 0,34458 | 0,34090 | 0,33724 | 0,33360 | 0,32997 | 0,32636 | 0,32276 | 0,31918 | 0,31561 | 0,31207 |
| -0,3 | 0,38209 | 0,37828 | 0,37448 | 0,37070 | 0,36693 | 0,36317 | 0,35942 | 0,35569 | 0,35197 | 0,34827 |
| -0,2 | 0,42074 | 0,41683 | 0,41294 | 0,40905 | 0,40517 | 0,40129 | 0,39743 | 0,39358 | 0,38974 | 0,38591 |
| -0,1 | 0,46017 | 0,45620 | 0,45224 | 0,44828 | 0,44433 | 0,44038 | 0,43644 | 0,43251 | 0,42858 | 0,42465 |
| -0,0 | 0,50000 | 0,49601 | 0,49202 | 0,48803 | 0,48405 | 0,48006 | 0,47608 | 0,47210 | 0,46812 | 0,46414 |

A tabela Z é composta por duas colunas principais:
Valor Z: Esta coluna lista os valores de Z, que representam o número de desvios padrão acima (positivos) ou abaixo (negativos) da média zero.
Área Sob a Curva Normal: Esta coluna fornece a área sob a curva normal à esquerda do valor Z correspondente. Essa área representa a probabilidade acumulada de obter um valor menor que Z em uma distribuição normal padrão.
Para usar a tabela Z, você segue os seguintes passos:
- Localize o valor Z calculado na coluna “Valor Z” da tabela Z.
- Leia a probabilidade associada a esse valor Z na coluna “Área Sob a Curva Normal”. Essa probabilidade representa a chance de obter um valor menor que Z em uma distribuição normal padrão.
Exemplo de Z-score para 1.14

A tabela Z é uma ferramenta essencial para realizar testes de hipóteses, calcular intervalos de confiança e realizar análises estatísticas que envolvem a distribuição normal. Ela permite que os analistas determinem rapidamente a probabilidade de eventos específicos ocorrerem em uma distribuição normal padrão, o que é fundamental para tomada de decisões baseadas em dados e inferência estatística.
Hoje em dia, com o uso de software estatístico, a consulta à tabela Z é menos comum, mas ainda é uma base importante para entender os conceitos estatísticos subjacentes.
Após calcular a estatística do teste Z, você pode compará-la a um valor crítico de Z (obtido a partir de tabelas de distribuição normal padrão) ou usar software estatístico para encontrar o valor p associado. Use esta tabela Z, também conhecida como tabela de escores Z, tabela de distribuição normal padrão e gráfico de valores Z, para encontrar um escore Z.
Em posse do número de Z basta acessar a tabela de Z e buscar o número do Z-score da seguinte forma:
O valor p representa a probabilidade de obter a estatística do teste Z observada (ou mais extrema) sob a hipótese nula.
- Se o valor p for menor que o nível de significância escolhido (geralmente 0,05), você rejeitará a hipótese nula (H0) em favor da hipótese alternativa (H1). Isso significa que há evidências estatísticas para a diferença entre a média da amostra e a média populacional (ou média de referência).
- Se o valor p for maior que o nível de significância, você não terá evidências estatísticas suficientes para rejeitar a hipótese nula, o que sugere que não há diferença estatisticamente significativa.
O Teste Z é uma ferramenta útil para análises comparativas, como testar se a média de um grupo de amostra difere da média populacional ou da média de outro grupo. No entanto, é importante lembrar que as premissas do teste devem ser atendidas para que os resultados sejam confiáveis. Se as premissas não forem atendidas, outras técnicas estatísticas podem ser necessárias.
Cauda inferior (lower tail), cauda superior (upper tail) ou bicaudal (two-tailed)
Em seguida, a estatística do teste é usada para realizar o teste de hipóteses, usando ou a abordagem do valor-p (p-value) ou a abordagem do valor crítico (critical value).
Os passos específicos adotados em cada abordagem dependem principalmente da forma do teste de hipóteses: cauda inferior (lower tail), cauda superior (upper tail) ou bicaudal (two-tailed). A forma do teste pode ser facilmente identificada olhando para a hipótese alternativa (Ha).

Aqui estão as diretrizes gerais para identificar a forma do teste com base na hipótese alternativa:
- Se a hipótese alternativa (Ha) contém um sinal de menor que (<), é um teste de cauda inferior (lower tail). Nesse caso, estamos interessados em provar que a estatística do teste é menor do que um determinado valor crítico.
- Se a hipótese alternativa (Ha) contém um sinal de maior que (>), é um teste de cauda superior (upper tail). Aqui, estamos tentando mostrar que a estatística do teste é maior do que um valor crítico específico.
- Se a hipótese alternativa (Ha) contém um sinal de desigualdade diferente de (≠), é um teste bicaudal (two-tailed). Isso significa que estamos interessados em detectar qualquer diferença significativa, seja menor ou maior do que um valor crítico.

Com base nessa identificação da forma do teste, podemos prosseguir com a abordagem do valor-p, onde a estatística do teste é usada para calcular um valor-p, ou com a abordagem do valor crítico, onde a estatística do teste é comparada com um valor crítico predefinido.
Em resumo, a escolha entre as abordagens de valor-p e valor crítico depende da forma do teste, que, por sua vez, é determinada pela hipótese alternativa. A análise estatística é conduzida de acordo com a forma específica do teste.
Abordagem utilizando o valor de p (p-value)
O valor de p é uma medida estatística que avalia a probabilidade de obter resultados tão extremos ou mais extremos do que os observados, supondo que a hipótese nula seja verdadeira. É como um indicador de quão confiáveis são os dados que você está analisando.
Se o valor de p for baixo, isso sugere que os resultados são estatisticamente significativos e podem ser confiáveis para tomar decisões de negócios. Se for alto, pode indicar que os resultados podem ter ocorrido por acaso e devem ser interpretados com cautela.

Na abordagem do valor-p (p-value), a estatística do teste é usada para calcular um valor-p. A interpretação do valor-p depende do tipo de teste de hipóteses:
Teste de Cauda Inferior (Lower Tail): Se o teste for de cauda inferior, o valor-p é a probabilidade de obter um valor para a estatística do teste pelo menos tão pequeno quanto o valor observado na amostra. Em outras palavras, é a probabilidade de observar resultados tão extremos ou mais extremos do que os observados, assumindo que a hipótese nula (H0) seja verdadeira.

Teste de Cauda Superior (Upper Tail): Se o teste for de cauda superior, o valor-p é a probabilidade de obter um valor para a estatística do teste pelo menos tão grande quanto o valor observado na amostra. Novamente, isso implica que estamos avaliando a probabilidade de observar resultados tão extremos ou mais extremos, sob a suposição de que H0 seja verdadeira.

Teste Bicaudal (Two-Tailed): Em um teste bicaudal, o valor-p é a probabilidade de obter um valor para a estatística do teste tão improvável quanto o valor observado na amostra, seja na cauda inferior ou superior da distribuição. Isso significa que estamos considerando a probabilidade de observar diferenças significativas em ambas as direções, em relação à hipótese nula.

Em todos os casos, um valor-p baixo (geralmente menor que um nível de significância predefinido, como 0,05) sugere que temos evidências estatísticas para rejeitar a hipótese nula (H0). Quanto menor o valor-p, mais forte é a evidência contra a H0. Por outro lado, um valor-p alto indica que não temos evidências suficientes para rejeitar H0.
O valor-p é uma medida importante para tomar decisões estatísticas em testes de hipóteses e é usado para determinar se os resultados observados são estatisticamente significativos.
Tomada de decisão na abordagem do p-value
Na abordagem do valor-p (p-value), a tomada de decisão em relação à hipótese nula (H0) é baseada na comparação do valor-p com o nível de significância (α) predefinido:
- Se o valor-p for menor ou igual ao nível de significância (α), rejeita-se a hipótese nula (H0). Isso indica que há evidências estatísticas suficientes para suportar a hipótese alternativa (Ha).
- Se o valor-p for maior que o nível de significância (α), não se rejeita a hipótese nula (H0). Nesse caso, não há evidências estatísticas significativas para apoiar Ha, e a H0 é mantida.
Essa abordagem não muda, independentemente de ser um teste de cauda inferior, cauda superior ou teste bicaudal. A decisão de rejeitar ou não a hipótese nula depende exclusivamente da relação entre o valor-p e o nível de significância.
Abordagem utilizando o valor crítico (critical value):
O nível de significância (α) é usado para calcular o valor crítico.
Em um teste de cauda inferior, o valor crítico é o valor da estatística do teste que fornece uma área de α na cauda inferior da distribuição amostral da estatística do teste.

Em um teste de cauda superior, o valor crítico é o valor da estatística do teste que fornece uma área de α na cauda superior da distribuição amostral.

Em um teste bicaudal, existem dois valores críticos, um na cauda inferior e outro na cauda superior, cada um fornecendo uma área de α/2 em suas respectivas caudas da distribuição amostral.

Após calcular os valores críticos, você compara a estatística do teste obtida na amostra com esses valores críticos. Se a estatística do teste for maior que o valor crítico na cauda superior ou menor que o valor crítico na cauda inferior (ou fora dos dois valores críticos em um teste bicaudal), você rejeita a hipótese nula (H0). Caso contrário, você não rejeita H0.
Tomada de decisão na abordagem do valor crítico
Na abordagem do valor crítico (critical value), a decisão sobre a hipótese nula (H0) depende da comparação entre o valor crítico e a estatística do teste obtida na amostra. A decisão é tomada de acordo com a forma específica do teste de hipóteses:
Teste de Cauda Inferior (Lower Tail): Se o teste for de cauda inferior, você compara a estatística do teste com o valor crítico na cauda inferior da distribuição amostral. Se a estatística do teste for menor ou igual ao valor crítico, rejeita-se a hipótese nula (H0).

Teste de Cauda Superior (Upper Tail): Se o teste for de cauda superior, você compara a estatística do teste com o valor crítico na cauda superior da distribuição amostral. Se a estatística do teste for maior ou igual ao valor crítico, rejeita-se a hipótese nula (H0).

Teste Bicaudal (Two-Tailed): Em um teste bicaudal, você compara a estatística do teste com os valores críticos na cauda inferior e na cauda superior da distribuição amostral. Se a estatística do teste for menor ou igual ao valor crítico na cauda inferior OU maior ou igual ao valor crítico na cauda superior (ou seja, fora da região entre os dois valores críticos), rejeita-se a hipótese nula (H0).

Essa abordagem difere da abordagem do valor-p, onde a decisão de rejeitar ou não a hipótese nula é baseada na comparação entre o valor-p e o nível de significância (α), independentemente da forma do teste.
No método do valor crítico, a decisão depende do relacionamento direto entre a estatística do teste e os valores críticos especificados com base no nível de significância e na forma do teste. É importante escolher a abordagem apropriada com base nas características do teste de hipóteses que está sendo conduzido.
Erros em Hipóteses
Em testes de hipóteses estatísticas, os erros são situações nas quais as conclusões tiradas a partir dos dados amostrais podem estar incorretas. Existem dois tipos principais de erros que podem ocorrer em testes de hipóteses: erro do Tipo 1 (também chamado de erro alfa) e erro do Tipo 2 (também chamado de erro beta).

Erro do Tipo 1 (Erro Alfa):
O erro do Tipo 1 ocorre quando uma hipótese nula verdadeira é erroneamente rejeitada. Em outras palavras, é um falso positivo.
Probabilidade de Ocorrência: A probabilidade de cometer um erro do Tipo 1 é geralmente representada pelo nível de significância (alfa, α) escolhido para o teste. Um valor comum para α é 0,05, o que significa que há uma chance de 5% de cometer um erro do Tipo 1 ao rejeitar a hipótese nula.
Consequências: Rejeitar erroneamente uma hipótese nula verdadeira pode levar a conclusões incorretas e ações inadequadas.
Erro do Tipo 2 (Erro Beta):
O erro do Tipo 2 ocorre quando uma hipótese nula falsa não é rejeitada. Em outras palavras, é um falso negativo.
Probabilidade de Ocorrência: A probabilidade de cometer um erro do Tipo 2 é representada pela letra beta (β).
Consequências: Não rejeitar a hipótese nula quando ela é falsa significa que não detectamos um efeito real que existe nos dados. Isso pode levar a conclusões incorretas de que não há diferença ou efeito quando na verdade existe.
Erro do Tipo 1 (Erro Alfa) envolve a rejeição incorreta de uma hipótese nula verdadeira e é controlado pelo nível de significância (α) escolhido para o teste.
Erro do Tipo 2 (Erro Beta) envolve a não rejeição incorreta de uma hipótese nula falsa e é influenciado pelo poder do teste (1 – β).

Ao planejar um teste de hipóteses, você deve tentar equilibrar a minimização do erro do Tipo 1 (para evitar conclusões precipitadas) e a minimização do erro do Tipo 2 (para evitar a não detecção de efeitos reais).
Isso envolve escolher um nível de significância apropriado e, se possível, aumentar o tamanho da amostra para aumentar o poder do teste e reduzir o erro do Tipo 2. O poder do teste é a capacidade do teste de detectar uma diferença ou efeito quando ele realmente existe.
Conclusão
Realizar um teste de hipóteses é fundamental porque eles oferecem um método científico e estatístico para tomada de decisões informadas. Através desses testes, as pessoas podem avaliar a validade de suposições e fundamentar suas conclusões em evidências objetivas.
No contexto dos negócios, o testes de hipóteses desempenham um papel crucial na otimização de estratégias, na identificação de oportunidades de melhoria e na mitigação de riscos.
Esse teste capacita empresas a tomar decisões baseadas em dados, seja para lançar um novo produto, ajustar preços, aprimorar processos ou direcionar campanhas de marketing, garantindo uma abordagem mais precisa e eficaz para alcançar metas e maximizar o sucesso no mercado competitivo.
Referências:
- Andrew Bruce, Peter Bruce. Estatística prática para cientistas de dados: 50 conceitos essenciais. Edição Português. Alta Books, 1 julho 2019.
- Sample Size Determination and Power, Tom Ryan (Wiley, 2013)
- https://pt.wikipedia.org/wiki/Teorema_central_do_limite
- https://www.inf.ufsc.br/~andre.zibetti/probabilidade/normal.html
- https://www.grammarly.com/blog/how-to-write-a-hypothesis/
- https://www.inf.ufsc.br/~andre.zibetti/probabilidade/teste-de-hipoteses.html
- https://pt.wikipedia.org/wiki/Hip%C3%B3tese
- https://pt.wikipedia.org/wiki/Teste_Z
- https://en.wikipedia.org/wiki/P-value
- https://www.statssolver.com/hypothesis-testing.html
- https://pt.wikipedia.org/wiki/Hip%C3%B3tese_nula
- https://www.youtube.com/watch?v=tM0yVvcK2hI
- https://blog.proffernandamaciel.com.br/parametros-e-estatisticas/
- https://flowingdata.com/2014/05/09/type-i-and-ii-errors-simplified/
- https://www.statisticsteacher.org/2017/09/15/what-is-power/
- https://towardsdatascience.com/5-ways-to-increase-statistical-power-377c00dd0214
- http://daniellakens.blogspot.com/2014/12/observed-power-and-what-to-do-if-your.html
- https://www.youtube.com/watch?v=-ZU7fbvSJ60
- https://www.z-table.com/