Detalhes do projeto
- Link do projeto no Github: https://github.com/cerqueiralex/machine-learning-previsao-aluguel
- Tecnologias: Python, Pandas, Numpy, Matplotlib, Seaborn,Statsmodels, Scikit learn
- Categorias: Estatística
Este é um projeto de análise estatística exploratória utilizando o statsmodels e scikitlearn com uma base de dados fictícia para trabalhar o seguinte problema: Existe alguma relação entre a área de imóveis (em metros quadrados) e o valor do aluguel em uma determinada cidade? Caso exista relação, como podemos mensurá-la?
Para atacar esse problema de forma didática, primeiro iremos realizar uma análise estatística exploratória com regressão linear simples através do método Ordinary Least Squares que será explicado mais adiante e em seguida utilizaremos o mesmo método para treinar um modelo de previsão de machine learning que irá tentar prever o provável valor de um aluguel baseado na area em m² de um imóvel.
Primeiro as bibliotecas que iremos trabalhar:
# Imports
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_splitO objetivo inicial é utilizar as bibliotecas do pandas para importar os dados, matplotlib e seaborn para gerar alguns gráficos exploratórios e o statsmodels pra fazer uma regressão linear simples na fase analítica.
Em seguida utilizamos o numpy para criar os arrays de machinelearning e o sklearn para treinar o modelo e realizar um deploy.
Carregando os dados e fazendo análise exploratória
Carregamos então o dataset em csv e analisamos sua estrutura
# Carrega o dataset
df_dsa = pd.read_csv('dataset.csv')
df = pd.read_csv(path)
df.describeEsse é um pequeno dataset como podemos ver que possui somente 3000 linhas x 7 colunas

O dataset possui diversas dimensões, porém somente iremos utilizar o valor do aluguel e a área em m2. Como pode ver, essas são as dimensões disponíveis no dataset:
- ‘valor_aluguel’,
- ‘area_m2’,
- ‘ano_construcao’,
- ‘codigo_localidade’,
- ‘numero_banheiros’,
- ‘numero_cozinhas’,
- ‘codigo_bairro’

Agora vamos analisar qual é o valor médio dos aluguéis com o comando histplot:
# sns.histplot = chama o método histplot do seaborn
sns.histplot(data = df, x = "valor_aluguel", kde = True)
É possível observar que a maior parte dos valores de aluguel gira em torno da casa dos 300 a 400 reais.
Através do método “corr” podemos facilmente analisar uma matriz de correlação entre as dimensões do nosso dataset para entender o valor que iremos trabalhar com nossas dimensões de entrada e saída.
# Correlação entre as variáveis
df.corr()
O coeficiente de correlação é uma medida estatística que indica a força e a direção da relação linear entre duas variáveis numéricas. Ele varia entre -1 e 1, onde:
Um coeficiente de correlação igual a 1 indica uma correlação linear perfeita positiva, ou seja, quando uma variável aumenta, a outra variável também aumenta na mesma proporção.
Um coeficiente de correlação igual a -1 indica uma correlação linear perfeita negativa, ou seja, quando uma variável aumenta, a outra variável diminui na mesma proporção.
Um coeficiente de correlação igual a 0 sugere que não há correlação linear entre as duas variáveis.
O coeficiente de correlação mais comum é o de Pearson, que mede a correlação linear entre duas variáveis. Existem outras medidas de correlação, como o coeficiente de correlação de Spearman, que avalia a relação monotônica entre duas variáveis, e o coeficiente de correlação de Kendall, que considera a concordância entre os rankings das variáveis.
Nesse caso temos uma correlação de 58% que é bem fraca.
Agora vamos visualizar isso em um gráfico scatterplot para analisar a distribuição desses dados nas dimensões x e y.
# Vamos analisar a relação entre a variável de entrada area_m2 e a variável alvo valor_aluguel
sns.scatterplot(data = df_dsa, x = "area_m2", y = "valor_aluguel")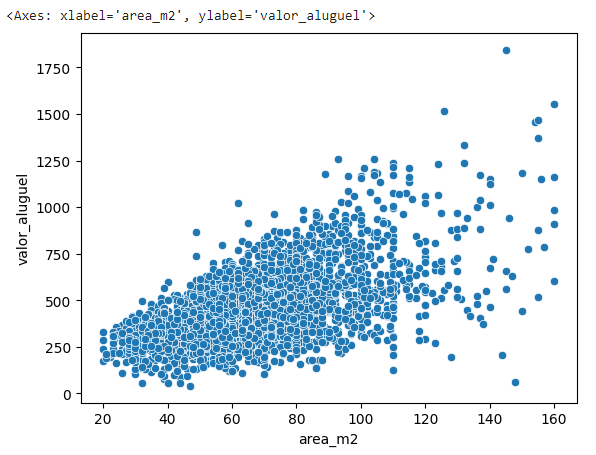
Regressão Linear Simples
A Regressão Linear é uma técnica estatística utilizada para modelar a relação entre uma variável dependente (também chamada de variável resposta ou variável alvo) e uma ou mais variáveis independentes (também chamadas de variáveis explicativas ou preditoras).
A Regressão Linear tem como objetivo estimar os coeficientes da equação que melhor descreve essa relação, minimizando a soma dos erros quadráticos entre os valores observados e os valores previstos pelo modelo.
Existem dois tipos principais de regressão linear:
Regressão Linear Simples: Neste caso, há apenas uma variável independente envolvida. A equação da Regressão Linear Simples é expressa como:
Y = a + bX + ε
Onde Y é a variável dependente, X é a variável independente, a é o coeficiente linear (intercepto), b é o coeficiente angular (inclinação) e ε é o erro aleatório.
Regressão Linear Múltipla: Neste caso, há duas ou mais variáveis independentes envolvidas. A equação é expressa como:
Y = a + b1X1 + b2X2 + … + bnXn + ε
Onde Y é a variável dependente, X1, X2, …, Xn são as variáveis independentes, a é o coeficiente linear (intercepto), b1, b2, …, bn são os coeficientes angulares (inclinações) e ε é o erro aleatório.
A Regressão Linear é amplamente utilizada em diversas áreas, como economia, ciências sociais, biologia e engenharia, para prever resultados, avaliar relações causais e identificar fatores que contribuem para um fenômeno específico.
Além disso, é uma técnica fundamental para a análise de dados e aprendizado de máquina, onde é usada para desenvolver modelos preditivos.
Construção do Modelo OLS (Ordinary Least Squares) com Statsmodels em Python
Ordinary Least Squares Regression (OLSR): uma técnica de regressão linear usada para minimizar a soma dos erros quadrados entre a variável dependente e as variáveis independentes.
O método sm.OLS(y, X) é uma função do pacote Statsmodels, biblioteca Python utilizada para análise estatística. A função OLS (Ordinary Least Squares) é usada para ajustar um modelo de regressão linear, minimizando a soma dos erros quadráticos entre os valores observados e os valores previstos pelo modelo.
A função sm.OLS(y, X) recebe dois argumentos principais:
y: Um array ou pandas Series representando a variável dependente (variável resposta ou alvo). É a variável que você deseja prever ou explicar com base nas variáveis independentes.
X: Um array ou pandas DataFrame representando as variáveis independentes (variáveis explicativas ou preditoras). São as variáveis que você deseja usar para explicar ou prever a variável dependente.
# Definimos a variável dependente
y = df_dsa["valor_aluguel"]
# Definimos a variável independente
X = df_dsa["area_m2"]
# O Statsmodels requer a adição de uma constante à variável independente
X = sm.add_constant(X)
# Criamos o modelo
modelo = sm.OLS(y, X)Em seguida treinamos o modelo e imprimimos o resultado:
# Treinamento do modelo
resultado = modelo.fit()
print(resultado.summary())E esse é o resultado do nosso modelo:

Interpretando o Resultado do Modelo Estatístico com Statsmodels
A tabela acima traz um resumo do modelo com diversas estatísticas. Aqui faremos a análise de uma delas, o R².
O coeficiente de determinação, também conhecido como R², é uma medida estatística que avalia o quão bem o modelo de regressão se ajusta aos dados observados. Ele varia de 0 a 1 e representa a proporção da variação total da variável dependente que é explicada pelo modelo de regressão.
A interpretação do R² é a seguinte:
R² = 0: Neste caso, o modelo de regressão não explica nenhuma variação na variável dependente. Isso significa que o modelo não é útil para prever ou explicar a variável de interesse.
R² = 1: Neste caso, o modelo de regressão explica toda a variação na variável dependente. Isso indica que o modelo se ajusta perfeitamente aos dados e é extremamente útil para prever ou explicar a variável de interesse.
0 < R² < 1: Neste caso, o modelo de regressão explica uma parte da variação na variável dependente. Quanto maior o valor de R², melhor o modelo se ajusta aos dados e melhor é a sua capacidade de prever ou explicar a variável de interesse.
É importante notar que um R² alto não garante que o modelo seja adequado, nem que haja uma relação causal entre as variáveis. Um R² alto pode ser resultado de variáveis irrelevantes, multicolinearidade ou até mesmo de um ajuste excessivo (overfitting). Portanto, é essencial avaliar outras estatísticas e diagnosticar o modelo antes de tirar conclusões definitivas.
Vamos plotar em um scatterplot os dados do modelo treinado para tirar uma conclusão:
# Plot
plt.figure(figsize = (12, 8))
plt.xlabel("area_m2", size = 16)
plt.ylabel("valor_aluguel", size = 16)
plt.plot(X["area_m2"], y, "o", label = "Dados Reais")
plt.plot(X["area_m2"], resultado.fittedvalues, "r-", label = "Linha de Regressão (Previsões do Modelo)")
plt.legend(loc = "best")
plt.show()
Claramente existe uma forte relação entre a área (em m2) dos imóveis e o valor do aluguel. Entretanto, apenas a área dos imóveis não é suficiente para explicar a variação no valor do aluguel, pois nosso modelo obteve um coeficiente de determinação (R²) de apenas 0.34.
O ideal seria usar mais variáveis de entrada para construir o modelo a fim de compreender se outros fatores influenciam no valor do aluguel.
É sempre importante deixar claro que correlação não implica causalidade e que não podemos afirmar que o valor do aluguel muda apenas devido à área dos imóveis. Para estudar causalidade devemos aplicar Análise Causal.
Em um Projeto de Regressão devemos validar as suposições (que são várias) antes de usar o modelo para tirar conclusões.
Treinando um modelo para previsão do valor do aluguel baseado na area em m2 usando Scikit Learn
Sabemos que com um valor de r² de baixa correlação observado (0.34) não é suficiente para treinar um modelo, mas como o objetivo desse projeto é somente exploratório, vamos prosseguir mesmo assim.
Vamos treinar o modelo usando a mesma técnica de regressão linear com Ordinary Least Squares.
Vamos então preparar nossa variável de entrada X e tranformá-la em um array numpy, fazer o reshape dela em um intervalo de -1 e 1 e definir nossa variável de saída Y como o valor do aluguel.
X = np.array (df['area_m2'])
X = X.reshape(-1,1)
Y = df['valor_aluguel']Em seguida vamos fazer um split no nosso modelo para um ambiente de teste e outro de treino. a amostra de testes será configurada para alocar 20% dos dados e consequentemente o treino será realizado com 80% dos dados.
X_treino, X_teste, Y_treino, Y_teste = train_test_split (X, Y, test_size = 0.2, random_state= 42)O shape das nossas variáveis ficou dessa forma:

Valor agora criar e treinar o modelo
modelo = LinearRegression()
modelo.fit(X_treino, Y_treino)Conseguimos agora analisar a curva da regressão já com a previsão do modelo
plt.scatter(X,Y)
plt.plot(X,modelo.predict(X), color = "red")
plt.xlabel("area em m2")
plt.ylabel ("valor do aluguel")
Vejamos o score do nosso modelo:
score = modelo.score(X_teste,Y_teste)
print(score)o nosso modelo ficou com um score de 0.3528410684969181 o que é um valor bem abaixo da média. Na prática esse modelo não poderia ser utilizado para realizar previsões, mas vamos ver como ele se sai.
O próximo passo agora é definir nossos vetores de intercepto (w0) e coeficiente (w1) da reta de regressão. Aqui um gráfico com uma breve explicação dos vetores que estaremos criando dentro do contexto da regressão:

modelo.intercept_ #W0
modelo.coef_ #W1Fazendo deploy do modelo
Agora com o modelo treinado, iremos utilizar um input qualquer de area em m2 para que nosso modelo faça a previsão de qual seria um provável valor de aluguel.

Conclusão
Apesar de ser um modelo preditivo fraco, conseguimos gerar algumas previsões a título de conhecimento e treino.
Como é possível observar, segundo o modelo, um imóvel de 500 m² teria uma média de valor de aluguel de R$2520,00
seguem alguns exemplos de previsões geradas pelo modelo:
| Area em m2 | Valor do aluguel |
| 250 | 1328.94245948 |
| 300 | 1567.3343353 |
| 350 | 1805.72621111 |
| 400 | 2044.11808692 |
| 450 | 2282.50996273 |
| 500 | 2520.90183854 |
Referências