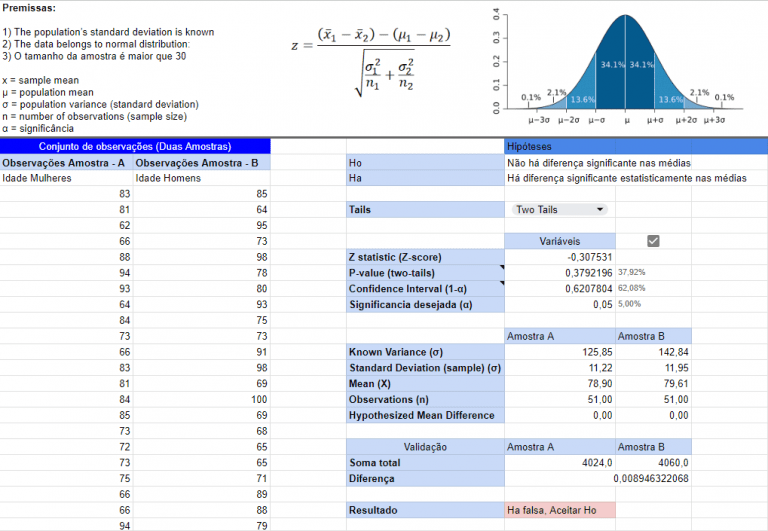
Matt Motyl, estudante de PhD em psicologia na University of Virginia em Charlottesville realizou um estudo com quase 2.000 pessoas e havia teoricamente descoberto que “extremistas políticos quase que literalmente viam o mundo em preto e branco”.
Os dados de seu estudo pareciam mostrar que os políticos moderados viam tons de cinza com mais precisão do que os extremistas de esquerda ou de direita. Ele parecia ter conseguido elaborar uma hipótese bem atraente do ponto de vista midiático e também dados que pareciam sustentar muito bem sua hipótese. O p-value deste experimento foi de 0,01 o que é considerado como “muito significativo” do ponto de vista da estatística inferencial. É como você afirmar que tem 99% de confiança no resultado estatístico de seu estudo.
Diante de tal resultado, era praticamente certo que Motyl estava a um passo de realizar uma publicação em um periódico de alto impacto.
Sensível às controvérsias sobre a reprodutibilidade, Motyl e seu consultor, Brian Nosek, decidiram replicar o estudo. Dessa vez com uma maior quantidade de dados, o p-value saiu como 0,59 – nem perto do padrão convencional de significância, 0,05, o que fez com que sua hipótese desabasse e seu estudo fosse por água a baixo.
Descobriu-se que o problema não estava nos dados ou nas análises da Motyl. Estava na natureza surpreendentemente escorregadia do p-value, que não é nem tão confiável nem tão objetiva quanto a maioria dos cientistas supõe. “Os p-values não estão fazendo seu trabalho, porque não podem”, diz Stephen Ziliak, economista da Roosevelt University em Chicago, Illinois, e um crítico frequente da maneira como as estatísticas são usadas.
A comunidade científica e o P < 0.05 como padrão de mercado para “comprovação” estatística
Em fevereiro de 2014, George Cobb, professor emérito de matemática e estatística no Mount Holyoke College, colocou as seguintes questões em um fórum de discussão da ASA (American Statistical Association):
P: Por que tantas faculdades e escolas de pós-graduação ensinam p = 0,05?
R: Porque ainda é o que a comunidade científica e os editores de periódicos usam.
P: Por que tantas pessoas ainda usam p = 0,05?
R: Porque foi isso que aprenderam na faculdade ou na pós-graduação.
Ou seja, tudo não parece passar de uma grande dependência circular que ocorre na área acadêmica como “Ensinamos porque é o que fazemos; fazemos isso porque é o que ensinamos.”
O número de artigos publicados no MEDLINE (base de dados da literatura internacional da área médica e biomédica) aumentou de 408.551 em 1990 para 1189.664 em 2014, um aumento relativo de 4,5% ao ano, e o número de resumos relatando pelo menos 1 p-value aumentou de 20.769 em 1990 (7,3%) para 138.654 em 2014 (15,6%), um aumento relativo de 8,2% ao ano.

O aumento na proporção de resumos com p-values ao longo do tempo pertence a todas as categorias, com aumentos mais proeminentes para metanálises (quase triplicando nas últimas 2 décadas).
Da mesma forma, entre os 385.393 artigos de PMC com p-values relatados no texto completo, 96,8% relataram pelo menos 1 p-value que era 0,05 ou menos, e essa proporção permaneceu estável ao longo do tempo com um crescimento que se retomou a partir de 2004.

Um dos principais motivos para esse fenômeno vem da sua origem por volta de 1920 através da publicação de Ronald Fisher.
Em 1925 Ronald Fisher um eminente matemático britânico publicou um dos livros mais influentes do século 20 sobre métodos estatísticos, o “Statistical Methods for Research Workers”. O método de Fisher é uma técnica de fusão de dados ou “meta análise” (análise de análises).
Este livro também popularizou o que é hoje o famoso p-value, que desempenha um papel central em sua abordagem. Fisher propõe o nível p = 0,05, ou uma chance de 1 em 20 de ser excedido por acaso, como um limite para significância estatística, e aplica isso a uma distribuição normal (como um teste de duas caudas), produzindo a regra de dois desvios padrão (em uma distribuição normal) para significância estatística.
A significância de 1,96, o valor aproximado do ponto percentil 97,5 da distribuição normal usada em probabilidade e estatística, também teve origem neste livro.

“O valor para o qual P = 0,05, ou 1 em 20, é 1,96 ou quase 2; é conveniente tomar este ponto como um limite para julgar se um desvio deve ser considerado significativo ou não.”
Segundo o próprio Fisher, o p-value = 0,05 é “conveniente” e não uma regra geral que deve ser seguida e aplicada a todos os experimentos.
Métricas complementares e o real impacto de um experimento
Suponha que você conduziu um experimento científico para desenvolver uma nova pílula de crescimento de cabelo, distribuindo para metade do seu grupo de cobaias uma pílula de placebo e para a outra metade a pílula que você deseja vender no mercado.
Ao final do experimento então você conclui um teste de significância estatística para comprovar que os novos fios de cabelo que cresceram foram por consequência da sua pílula e não por questões de chance e alcança um p-value de 0,05. E agora? Isso significa que você está pronto para colocar sua pílula à venda no mercado?
Não necessariamente, pois se nesse experimento, mesmo atingindo a significância estatística, o real resultado no período analisado (de 1 mês por exemplo) foi o crescimento de apenas 2 fios de cabelo, o impacto do seu produto é insignificante e portanto suas cobaias continuam calvas.
Uma breve introdução ao p-value e o teste de significância estatística
No teste de significância dentro da estatística inferencial, o p-value é a probabilidade de obter resultados de teste pelo menos tão extremos quanto o resultado realmente observado, sob a suposição de que a hipótese nula está correta. Um p-value muito pequeno significa que tal resultado extremo observado seria muito improvável de ocorrer em relação à hipótese nula.
Se apresentarmos apenas uma hipótese e o objetivo do teste estatístico for verificar se essa hipótese é sustentável, sem examinar outras hipóteses específicas, então esse teste é chamado de teste de hipótese nula.
O p-value é utilizado no contexto do teste de hipótese nula para medir a importância estatística de um resultado, que é o valor observado da estatística escolhida. Quanto menor o p-value, menor a probabilidade de obter esse resultado se a hipótese nula fosse verdadeira. Diz-se que um resultado é estatisticamente significativo se nos permite rejeitar a hipótese nula. Tudo mais sendo igual, p-values menores são considerados evidências mais fortes contra a hipótese nula.
Dizemos então que temos (1-α) ou (1-erro tipo I) de confiança para rejeitar a hipótese nula quando ela é realmente falsa.
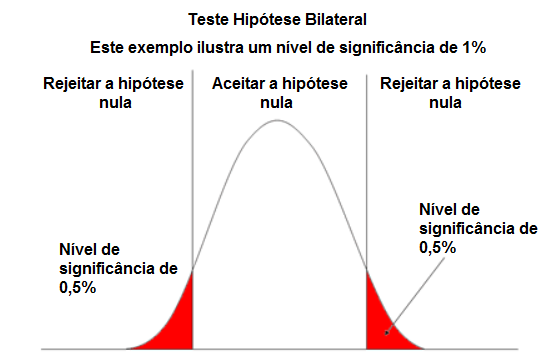
Em um teste de hipóteses, sempre partimos do pressuposto que a hipótese nula (H0) é verdadeira. Daí podemos tomar duas decisões:
- Aceitar H0 rejeitando Ha
- Aceitar Ha rejeitando H0
Porém é preciso nos atentar para não cometer alguns erros de análise comuns como rejeitar a hipótese nula quando ela é verdadeira, conhecido como Erro do Tipo I ou α (falso positivo), assim como aceitar a hipótese nula quando ela é falsa, conhecido como Erro do tipo II ou β (Falso negativo).

O fenômeno e os incentivos do P-hacking
Uma equipe de pesquisadores alemães descobriu que pessoas com uma dieta pobre em carboidratos perdiam peso 10% mais rápido se comessem uma barra de chocolate todos os dias. Essa pesquisa chegou à primeira página do Bild, o maior jornal diário da Europa, logo abaixo da atualização sobre o acidente da Germanwings.
A partir daí, começou a ser largamente compartilhado pela internet e além, virando notícia em mais de 20 países e meia dúzia de idiomas. Foi discutido em programas de notícias de televisão. O chocolate não apenas acelera a perda de peso, segundo o estudo, mas também leva a níveis de colesterol mais saudáveis e maior bem-estar geral. A história do Bild cita o principal autor do estudo, Johannes Bohannon, Ph.D., diretor de pesquisa do Instituto de Dieta e Saúde: “A melhor parte é que você pode comprar chocolate em qualquer lugar”.
Como foi que isso tudo aconteceu? Assim como o próprio condutor do estudo por trás dos chocolates disse em uma matéria para o Gizmodo “Aqui está um segredinho sujo da ciência: se você medir um grande número de coisas sobre um pequeno número de pessoas, é quase certo que obterá um resultado “estatisticamente significativo”.
Isso porque foram incluídos 18 indicadores diferentes a serem medidos, dentre eles, peso, colesterol, sódio, níveis de proteína no sangue, qualidade do sono, bem-estar, etc. de 15 pessoas.
Ou seja, é uma receita fácil para o fracasso da ferramenta de validação de significância, é a mesma coisa que você tentar provar que um vidro é a prova de balas arremessando contra ele uma bola de borracha. Você está conscientemente alterando as condições iniciais do experimento e afirmando um resultado que não representa a realidade.
Com tantos indicadores não independentes sendo medidos em paralelo dentro de um mesmo estudo, havia em torno de 60% de chance de obter algum resultado “significativo” com p < 0,05, podendo ser ainda menores.
Essa má prática é chamada de p-hacking – mexer com seu projeto experimental e dados para forçar um resultado de p abaixo de 0,05.
O site da five thirty eight criou um projeto de simulação em formato de paródia chamado “Hack Your Way To Scientific Glory” que consiste em uma simulação que te da um pequeno desafio onde você precisa através de algumas poucas seleções de dados encontrar uma correlação entre a quantidade de políticos de determinado partido americano e indicadores econômicos como empregabilidade, gdp, inflação e stock prices.

O projeto não passa de uma grande brincadeira (apesar dos dados serem reais) e mostra o quão fácil é você através de alguns dados encontrar correlação entre indicadores que não fazem o menor sentido, como por exemplo “mais republicanos no poder resultam em uma melhor economia” o que só reforça um problema clássico da estatística que é a confusão entre correlação e causalidade.
É possível provar estatisticamente por exemplo uma grande relação entre o crescimento do autismo desde o ano de 1997 nos estados unidos com o aumento das vendas de comida orgânica, mas será mesmo que isso faz algum sentido?

Um dos grandes desafios do mundo acadêmico é que nenhuma revista ou jornal deseja publicar artigos que não tenham resultados significativos, assim como nenhum acadêmico irá conseguir receber financiamento de instituições caso seus estudos não tenham uma fundação sólida, pois há muito dinheiro em jogo. Em último caso, há também um incentivo muito grande para atingir comprovação científica ou estatística como meio de avançar mais rápido na carreira.
Mas afinal, isso significa que validação de significância estatística é um erro e que não funciona de verdade? Deveríamos encontrar um substituto para essa ferramenta?
A declaração da American Statistical Association sobre a significância estatística e o uso do p-value
Quanto mais esse teste se popularizou e passou a ser utilizado largamente pela comunidade científica, acadêmicos e estatísticos, naturalmente que muitos problemas passaram a surgir, assim como diversas más práticas e confusões ao redor desse tema.
Durante o período de 2010 a 2014 o conselho da ASA foi estimulado por diversas discussões e críticas de grande visibilidade nos últimos anos citadas por grandes revistas e jornais do meio científico:
“É o segredinho sujo da ciência: o ‘método científico’ de testar hipóteses por meio de análises estatísticas tem uma base frágil.”
ScienceNews (Siegfried 2010)
“inúmeras falhas profundas” no teste de significância da hipótese nula.
Science News Wire (2013)
“técnicas estatísticas para testar hipóteses… têm mais falhas do que as políticas de privacidade do Facebook”.
ScienceNews (Siegfried 2014)
Neste mesmo período, o estatístico e blogueiro da “Simply Statistics” Jeff Leek respondeu em relação a essas controversias “O problema não é que as pessoas usam mal os p-values, é que a grande maioria da análise de dados não é realizada por pessoas adequadamente treinadas para realizar a análise de dados”
Nesse sentido, apenas confrontar diretamente esse mar de problemas causados pela má utilização e interpretação dos testes de significância não seria suficiente para resolver a raíz do problema, foi então que a ASA publicou uma declaração oficial para reforçar aos cientistas para que serve o p-value e como funciona o teste de significância estatística.
ASA: Definição do p-value
Informalmente, um p-value é a probabilidade sob um modelo estatístico especificado de que um resumo estatístico dos dados (por exemplo, a diferença média amostral entre dois grupos comparados) seja igual ou mais extremo do que seu valor observado.
ASA: Os 6 princípios
- Os p-values podem indicar o quão incompatíveis os dados são com um modelo estatístico especificado.
- Os p-values não medem a probabilidade de que a hipótese estudada seja verdadeira ou a probabilidade de que os dados tenham sido produzidos apenas por acaso.
- Conclusões científicas e decisões de negócios ou políticas não devem se basear apenas em se um p-values ultrapassa um limite específico.
- A inferência adequada requer relatórios completos e transparência
- Um p-value, ou significância estatística, não mede o tamanho de um efeito ou a importância de um resultado.
- Por si só, um p-value não fornece uma boa medida de evidência em relação a um modelo ou hipótese.
A declaração completa pode ser conferida aqui: https://amstat.tandfonline.com/doi/full/10.1080/00031305.2016.1154108#aHR0cDovL2Ftc3RhdC50YW5kZm9ubGluZS5jb20vZG9pL3BkZi8xMC4xMDgwLzAwMDMxMzA1LjIwMTYuMTE1NDEwOEBAQDA=
Conclusão
Os p-values não medem a probabilidade de que a hipótese estudada seja verdadeira ou a probabilidade de que os dados tenham sido produzidos por acaso.
Segundo a própria ASA “A boa prática estatística, como um componente essencial da boa prática científica, enfatiza os princípios de bom desenho e condução do estudo, uma variedade de resumos numéricos e gráficos de dados, compreensão do fenômeno em estudo, interpretação dos resultados no contexto, relatórios completos e lógica adequada e compreensão quantitativa do significado dos resumos de dados. Nenhum índice único deve substituir o raciocínio científico.”
Uma ênfase muito grande em alcançar determinada significância estatística acaba negligenciando diversos outros fatores e indicadores como o real impacto de um determinado experimento, ou a constância e a frequência com que aquele resultado se mantêm verdadeiro.
É imperativo também que os responsáveis por produzir tais experimentos saibam realizar uma análise de dados correta e mais ampla ao redor daquilo que estão produzindo e não ficar cego e refém de uma validação estatística apenas.
Assim como é sempre necessário por parte das mídias que irão veicular os resultados de estudos fazer uma diligência correta de suas matérias e evitar a veiculação de fake-news.
Referências
- https://jamanetwork.com/journals/jama/fullarticle/2503172
- https://journals.sagepub.com/doi/10.1177/1745691612459058
- https://amstat.tandfonline.com/doi/full/10.1080/00031305.2016.1154108#aHR0cDovL2Ftc3RhdC50YW5kZm9ubGluZS5jb20vZG9pL3BkZi8xMC4xMDgwLzAwMDMxMzA1LjIwMTYuMTE1NDEwOEBAQDA=
- https://jamanetwork.com/journals/jama/fullarticle/2503172
- https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4111019/
- https://en.wikipedia.org/wiki/P-value
- https://www.youtube.com/watch?v=42QuXLucH3Q
- https://www.youtube.com/watch?v=kTMHruMz4Is
- https://en.wikipedia.org/wiki/Ronald_Fisher
- https://gizmodo.com/i-fooled-millions-into-thinking-chocolate-helps-weight-1707251800
- https://projects.fivethirtyeight.com/p-hacking/