Muitos usuários consumidores de serviços de streaming de músicas como spotify ou do antigo ipod shuffle já passaram pela mesma dor de cabeça que é o fato de estar ouvindo aquela playlist favorita em modo aleatório e ter a sensação de que o algoritmo está repetindo muitas vezes os mesmos artistas ou as mesmas músicas de sempre, o que traz um certo desapontamento, pois no final das contas, nós temos geralmente uma expectativa de ouvir todas as diversas músicas que adicionamos com tanto carinho e que acabam sendo deixadas de lado ou tocando poucas vezes.
Essa sensação quando recorrente acaba levantando a dúvida em nossas cabeças sobre a real aleatoriedade do serviço, afinal se eu estou ouvindo em modo aleatório, porque as mesmas músicas repetem tantas vezes, enquanto as músicas que eu quero ouvir não tocaram nenhuma vez ainda?
Isso não é nenhuma novidade e os fóruns do spotify, do reddit e também do ipod shuffle estão lotados de reclamações a respeito dessa questão enquanto que os funcionários dessas empresas continuam dando sempre a mesma resposta de que seus algoritmos são aleatórios. Nesse caso, quem tem razão, as empresas ou os usuários?
A percepção da aleatoriedade
Observando a imagem abaixo, qual das duas sequências passa a você a impressão de mais aleatoriedade?
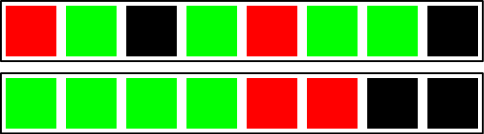
É natural do ser humano identificar a primeira sequência como sendo algo mais aleatório, pois as cores estão distribuídas de forma mais uniforme e separadas, porém a realidade é que qualquer uma das duas sequências pode ser considerada totalmente aleatória.
Suponha que você tenha criado uma playlist com 10 músicas da categoria “1”, 10 músicas da categoria “2”, 10 músicas da categoria “3” e por fim mais 10 músicas da categoria 4.
Ao simular uma sequência aleatória dessa playlist utilizando a função random.shuffle() da biblioteca random do python é possível obter as seguintes sequências como resultado:
[2, 3, 2, 2, 3, 2, 2, 3, 3, 1, 2, 1, 2,4, 3, 3, 1, 1, 1, 3, 4, 4, 1, 4, 3, 2, 4, 4, 4, 2, 4, 4, 1, 4, 3, 1, 3, 1, 2, 1]
[2, 1, 3, 4, 2, 3, 3, 3, 4, 1, 4, 1, 1, 4, 2, 1, 4, 1, 1, 2, 3, 3, 2, 2, 4, 3, 3, 4, 4, 3, 4, 1, 3, 2, 2, 1, 2, 2, 4, 1]
[4, 3, 2, 3, 3, 4, 3, 2, 2, 3, 1, 4, 2, 1, 4, 4, 2, 4, 3, 2, 2, 1, 1, 1, 4, 1, 1, 2, 1, 2, 1, 2, 4, 3, 3, 1, 4, 4, 3, 3]
[1, 3, 3, 2, 3, 1, 2, 3, 3, 4, 2, 2, 2, 2, 2, 2, 3, 3, 1, 3, 1, 4, 4, 3, 4, 1, 1, 2, 1, 4, 4, 1, 4, 1, 4, 4, 1, 2, 4, 3]
[4, 2, 1, 3, 3, 1, 2, 4, 2, 4, 2, 2, 4, 1, 1, 1, 4, 3, 3, 2, 2, 1, 1, 4, 3, 3, 1, 4, 3, 3, 2, 4, 2, 2, 4, 4, 1, 3, 3, 1]
Repare que no caso do 4 resultado da 4 linha, existe uma sequencia de 6 números “2” seguidos. Quando falamos de um algoritmo realmente aleatório, isso não só é plenamente possível de acontecer, como é bem provável, pois o aleatório não possui memória, dessa forma cada evento é exclusivo e independente.
No primeiro resultado da primeira linha (azul), apesar de não ter ocorrido uma sequência tão alta de números repetidos se comparados com a 4 linha, é interessante notar que se você estivesse ouvindo essa playlist e essa sequência tocasse, você ouviria 9 vezes o gênero “4” contra somente 2 músicas do gênero “1” , 2 do gênero “2” e 1 do gênero “3”, ou seja, 64% do tempo você iria ouvir músicas do gênero 4, o que passaria uma certa percepção de “não aleatoriedade”.
Um disclaimer sobre os dados gerados: A maioria dos dados aleatórios gerados com Python não são totalmente aleatórios no sentido científico da palavra. Em vez disso, é pseudoaleatório, ou seja, gerado por um gerador de números pseudoaleatórios (PRNG), que é essencialmente qualquer algoritmo para gerar dados aparentemente aleatórios, mas ainda reprodutíveis.
Números aleatórios “verdadeiros” podem ser gerados por um verdadeiro gerador de números aleatórios (TRNG) como por exemplo arremessar repetidamente um dado de verdade no chão na vida real. Supondo que seu lançamento seja imparcial, você realmente não tem ideia do número em que o dado cairá pois desconhece as variáveis envolvidas no processo. Jogar um dado é uma forma grosseira de usar hardware para gerar um número que não é determinístico.
A probabilidade de um arremesso de moeda
Considerando o lançamento repetido de uma moeda justa. Os resultados em diferentes lançamentos são estatisticamente independentes e a probabilidade de se obter cara em um único lançamento é de 1/2 ou 50%. A probabilidade de se obter duas caras em dois lançamentos é 1/4 ou 25% e a probabilidade de se obter três caras em três lançamentos é de1/8 ou 12,5%.
Ao simular o arremesso de 10 moedas em python da seguinte forma:
import random
def cointoss():
rand_i = random.randint(0, 1)
outcomes = ["Heads", "Tails"]
return outcomes[rand_i]
# Arremessa uma moeda 10 vezes
t1 = cointoss()
t2 = cointoss()
t3 = cointoss()
t4 = cointoss()
t5 = cointoss()
t6 = cointoss()
t7 = cointoss()
t8 = cointoss()
t9 = cointoss()
t10 = cointoss()
print(t1, t2, t3, t4, t5, t6, t7, t8, t9, t10)Obtive a seguinte sequência, onde “Heads” = cara e “Tails” = coroa:
Tails Tails Heads Tails Heads Heads Heads Heads Heads Heads
A probabilidade desse evento é de 1/(2^6) = 1/64 ou 0,015% e ainda sim consegui esse resultado após apenas 3 simulações.
A verdade sobre a probabilidade de se gerar um número aleatório como o arremesso de uma moeda, é que não importa quantas milhões vezes você a tenha jogado e não importa quantas sequências seguidas de caras ou coroas você obtenha, a probabilidade de se obter o resultado do outro lado sempre será de 50%. Então se você arremessar uma moeda justa 100 vezes e as 100 vezes ela tiver caído cara, isso em nada influencia a probabilidade do próximo arremesso sair coroa, que será sempre de 50%.
A Falácia do Apostador (The Gambler’s Falacy)
A falácia do apostador, também chamada de falácia de Monte Carlo ou falácia da maturidade das chances, é uma crença incorreta de que a probabilidade de um evento ocorrer no futuro é afetada por sua frequência passada.
Isso é incorreto porque a probabilidade de um evento não depende do que aconteceu antes, especialmente quando os eventos são estatisticamente independentes. Essa falácia é comumente associada aos jogos de azar, onde os jogadores podem acreditar que a probabilidade de uma determinada jogada ocorrer é afetada pelo histórico recente de jogadas.
O nome “falácia de Monte Carlo” vem de um exemplo que talvez seja o mais famoso desse fenômeno, ocorrido em um jogo de roleta no Monte Carlo Casino em 18 de agosto de 1913, quando a bola caiu na cor preta 26 vezes seguidas. Esta foi uma ocorrência extremamente incomum: a probabilidade de uma sequência de vermelho ou preto ocorrer 26 vezes seguidas é de (18/37)^26-1 ou cerca de 1 em 66,6 milhões, supondo que o mecanismo seja imparcial.
Os jogadores perderam milhões de francos apostando contra as casas pretas, pensando que esta sequencia estava causando um desequilíbrio na aleatoriedade da roda e que deveria ser seguida por uma longa sequencia de casas vermelhas.
Mas não precisamos ir tão longe pra perceber que essa falácia é comum e ainda é frequente nos dias de hoje, pois faz parte da nossa forma de perceber aquilo que é aleatório.
Basta ver os milhares de depoimentos de usuários apontando essa suposta “falha” nos algoritmos dos serviços de streaming de música:


Como é possível observar nestes e em milhares de outros exemplos, os usuários não gostam da sensação de uma real aleatoriedade, isso porque se você acabou de ouvir uma música de um determinado artista, isso não significa que a próxima música provavelmente será de um artista diferente em uma ordem perfeitamente “aleatória”.
Isso nos leva a crer que o que os usuários realmente buscam não é a aleatoriedade, mas sim uma uniformidade dos resultados.
A solução do Spotify para esse problema: um novo algoritmo
Desde que seu serviço foi lançado pela primeira vez, a Spotify utilizava o algoritmo de embaralhamento de Fisher-Yates nomeado em homenagem a Ronald Fisher e Frank Yates, que o descreveram pela primeira vez para gerar um embaralhamento virtualmente perfeito de uma playlist.
Também conhecido como o “embaralhamento de Knuth”, em homenagem a Donald Knuth esse algoritmo é utilizado para embaralhar sequências finitas, gerando uma permutação aleatória. O processo funciona colocando todos os elementos da sequência em um “chapéu” e, em seguida, selecionando aleatoriamente um elemento até que não haja mais nenhum elemento restante.
Cada permutação gerada pelo algoritmo de Fisher-Yates é imparcial, ou seja, todas as permutações são igualmente prováveis.
Esse algoritmo é eficiente e leva um tempo proporcional ao número de itens que estão sendo embaralhados, além de embaralhá-los no lugar.
O problema de utilizar um algoritmo aleatório virtualmente perfeito é que os eventos constatados anteriormente podem ocorrer, ocasionando em uma sequência irritante das mesmas músicas sendo tocadas repetidamente.
A solução então, não é melhorar o algoritmo tornando-o mais aleatório ainda, muito pelo contrário, torná-lo menos aleatório e mais uniforme.
Algoritmos de Dithering
O novo algoritmo implementado pelo Spotify se inspirou em algoritmos de Dithering, especialmente o Floyd–Steinberg dithering publicado pela primeira vez em 1976 por Robert W. Floyd e Louis Steinberg, o algoritmo de pontilhamento Floyd-Steinberg é amplamente utilizado por softwares de manipulação de imagens. Esse algoritmo é especialmente útil quando se deseja converter uma imagem em formato GIF, que é restrito a um máximo de 256 cores.
Esse tipo de algoritmo consiste basicamente em calcular a probabilidade de um pixel se tornar de uma determinada cor de uma paleta mais simples a depender da sua característica rgb mais complexa com o objetivo de reduzir a quantidade de cores em uma imagem e deixá-la mais leve.
Inspirado nisso, o algoritmo do Spotify segue uma regra semelhante da seguinte forma:
Suponha que você tem uma lista de reprodução contendo algumas músicas de The White Stripes, The xx, Bonobo, Britney Spears e Jaga Jazzist. Para cada artista, o algoritmo suas músicas e tenta estendê-las o mais uniformemente possível ao longo de toda a lista de reprodução. Em seguida, são coletadas todas as músicas e reordenadas se acordo com sua posição.
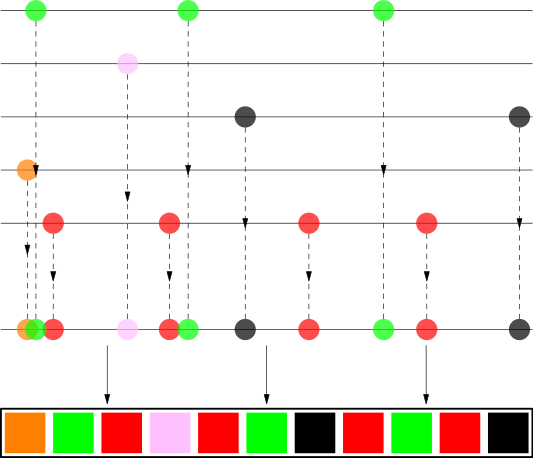
Como você pode ver, as músicas de um artista são bem espalhadas e parecem bastante aleatórias ao olho humano.
Digamos que temos 4 músicas do The White Stripes como na foto acima. Isso significa que eles devem aparecer aproximadamente a cada 25% da duração da lista de reprodução. São espalhadas as 4 músicas ao longo de uma linha, mas a distância varia aleatoriamente de cerca de 20% a 30% para tornar a ordem final mais aleatória. Você deve ser capaz de ver que a distância entre os círculos vermelhos na linha não é a mesma.
Foi introduzido um deslocamento aleatório no início; caso contrário, todas as primeiras músicas terminariam na posição 0. Você pode ver que Britney Spears e Jaga Jazzist têm apenas uma música, mas o deslocamento aleatório faz com que apareçam em um local aleatório na lista de reprodução.
Também foram embaralhadas as músicas do mesmo artista entre si, para evitar também que músicas do mesmo álbum sejam tocadas muito próximas umas das outras.
Em suma, o algoritmo é muito simples e pode ser implementado em apenas algumas linhas. Também é muito rápido, performático e produz resultados decentes.
Conclusão
Existem algoritmos de embaralhamento de música mais avançados por aí. O problema é que adicionar complexidade pode tornar os algoritmos mais lentos. O algoritmo do Spotify é simples, mas permite que as músicas sejam embaralhadas quase instantaneamente, sendo a performance um fator crucial no serviço.
O cérebro humano torna o conceito de “aleatório” difícil de se executar. O algoritmo é mais sobre criar a ilusão de aleatoriedade do que a verdadeira aleatoriedade, porque é isso que nossos cérebros querem.
Talvez nós utilizamos o termo “aleatoriedade” no lugar de alguma outra definição melhor que não sabemos ainda e que poderia ser melhor encaixado nesse tipo de contexto específico das nossas necessidades.
Referências
- https://engineering.atspotify.com/2014/02/how-to-shuffle-songs/
- https://en.wikipedia.org/wiki/Fisher%E2%80%93Yates_shuffle
- https://keyj.emphy.de/balanced-shuffle/
- https://en.wikipedia.org/wiki/Gambler’s_fallacy
- https://realpython.com/python-random/
- https://empiricalzeal.com/2012/12/21/what-does-randomness-look-like/
- https://en.wikipedia.org/wiki/Floyd%E2%80%93Steinberg_dithering

